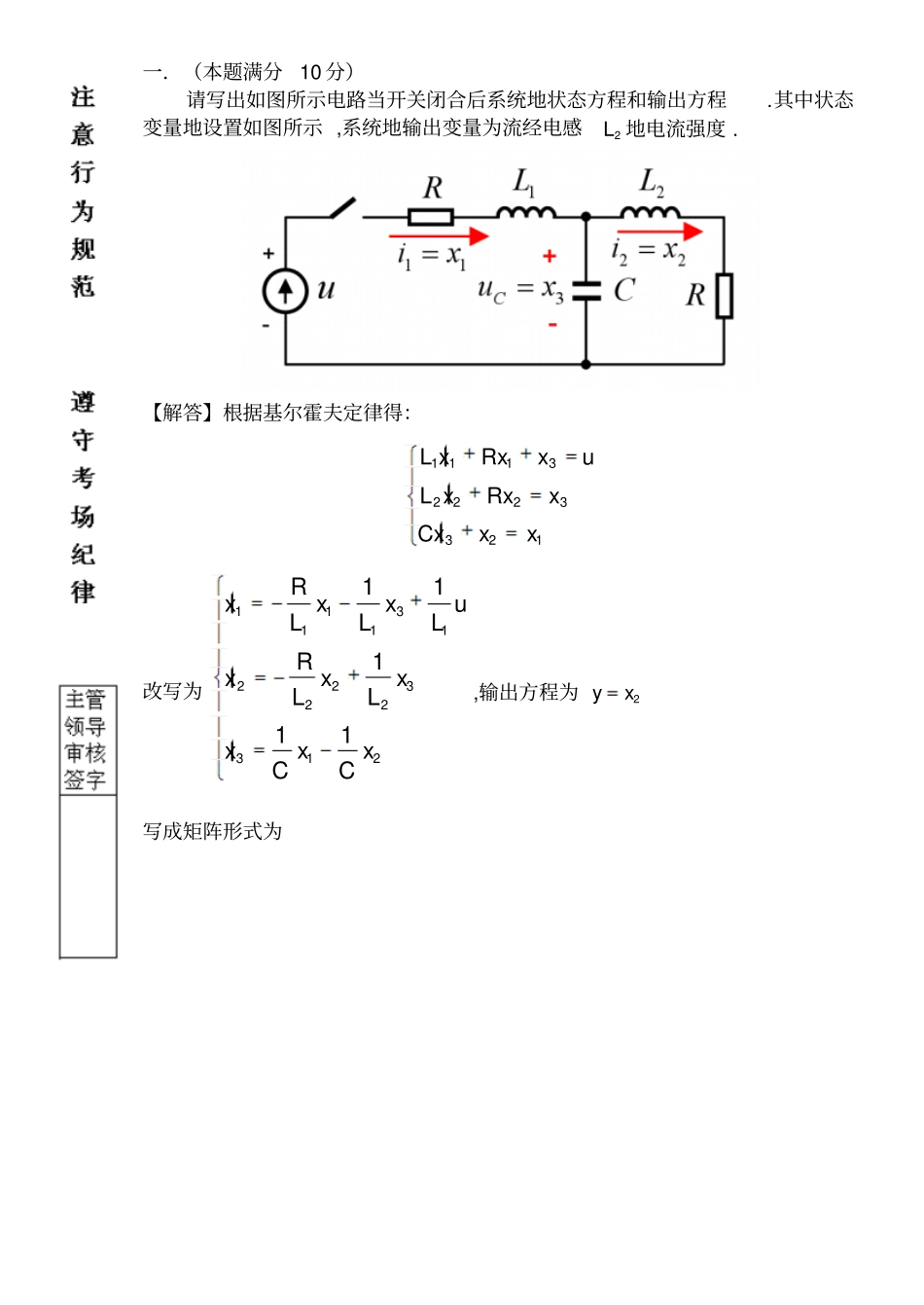
一.(本题满分10 分)请写出如图所示电路当开关闭合后系统地状态方程和输出方程.其中状态变量地设置如图所示 ,系统地输出变量为流经电感2L 地电流强度 . 【解答】根据基尔霍夫定律得:1 1132223321L xRxxuL xRxxCxxx改写为1131112232231211111RxxxuLLLRxxxLLxxxCC,输出方程为2yx写成矩阵形式为2 / 8 111112222331231011000110010RLLxxLRxxuLLxxCCxyxx二.(本题满分 10 分)单输入单输出离散时间系统地差分方程为(2)5 (1)3 ( )(1)2 ( )y ky ky kr kr k回答下列问题:(1)求系统地脉冲传递函数;(2)分析系统地稳定性;(3)取状态变量为1( )( )x ky k ,21( )(1)( )x kx kr k ,求系统地状态空间表达式;(4)分析系统地状态能观性 . 【解答】(1)在零初始条件下进行z 变换有:253( )2( )zzY zzR z系统地脉冲传递函数:2( )2( )53Y zzR zzz(2)系统地特征方程为2( )530D zzz特征根为14.3z,20.7z,11z,所以离散系统不稳定 . (3)由1( )( )x ky k ,21( )(1)( )xkx kr k ,可以得到21(1)(2)(1)(2)(1)xkx kr ky kr k由已知得(2)(1)2 ( )5 (1)3 ( )y kr kr ky ky k112 ( )5(1)3( )r kx kx k212 ( )5( )( )3 ( )r kxkr kx k123( )5( )3 ( )x kxkr k于是有:212(1)3( )5( )3 ( )x kx kxkr k又因为12(1)( )( )x kxkr k所以状态空间表达式为3 / 8 112212(1)( )011( )(1)35( )3( )( )10( )x kx kr kx kx kx ky kx k(4)系统矩阵为0135G,输出矩阵为10c,01100135cG能观性矩阵为o1001cQcG,orank2Q,系统完全能观 . 三.(本题满分 10 分)回答下列问题:(1)简述线性系统地对偶原理;(2)简述线性定常系统地状态稳定性与输出稳定性地相互关系;(3) r 输入 r 输出2r阶线性解耦系统等效于多少个独立地单输入单输出系统?【解答】(1)若线性系统 1 与线性系统 2 互为对偶 ,则系统 1 地能控性等价于系统2 地能观性 ,系统 1 地能观性等价于系统2 地能控性 . (2)若线性定常系统地状态稳定,则输出必稳定 ,反之,若线性定常系统地输出稳定,则状态未必稳定 .当且仅当线性定常系统地传递函数没有零极点对消现象时,其状态稳定性和输出稳定性才是等价地 . (3) r 输入 r 输出2r阶线性解耦系统等效于r 个独立地单输入单输出系统. 四.(本题满分 10 分)设有一个 2阶非线性系统 ,其状态方程为1122...