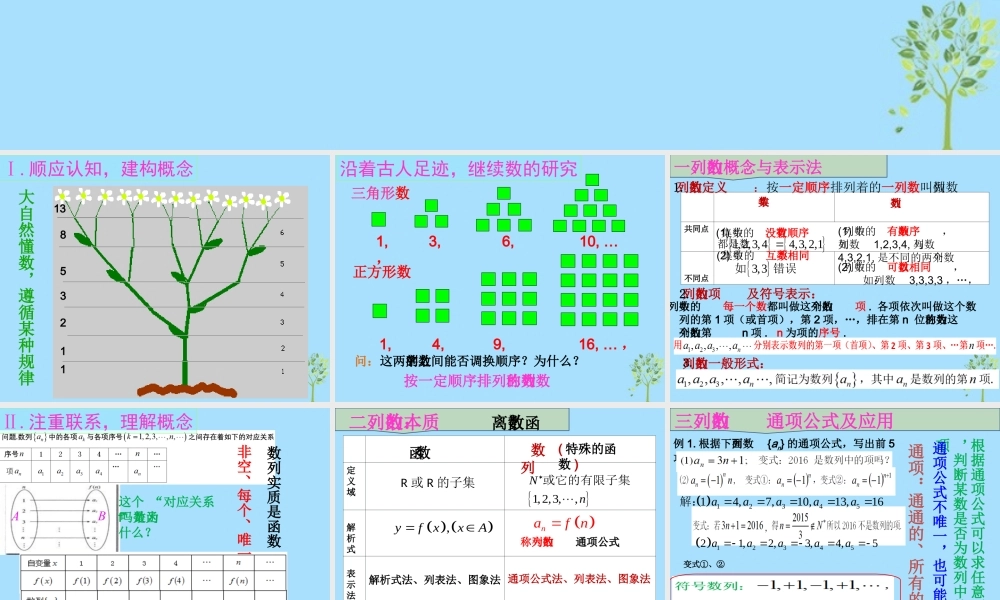
15328131Ⅰ. 顺应认知,建构概念大自然懂数,遵循某种规律1, 3, 6, 10, …, 1, 4, 9, 16, … , 沿着古人足迹,继续数的研究三角形数正方形数问:这两列数的数字之间能否调换顺序?为什么?按一定顺序排列的数称为数列 数列 数 列 集共同点 都是数不同点一、数列的概念与表示法1. 数列的定义:按一定顺序排列着的一列数叫做数列3,3如错误1,2,3,44,3,2,1数 集数 列(1) 数集中的数没有顺序(2) 数集中的数互不相同(1) 数列中的数有顺序,如数列1,2,3,4, 与数列 4,3,2,1, 是不同的两个数列(2) 数列中的数可以相同, 如:数列3,3,3,3 ,…,2. 数列的项及符号表示:⒊ 数列的一般形式:数列中的每一个数都叫做这个数列的项 . 各项依次叫做这个数列的第 1 项(或首项),第 2 项,…,排在第 n 位的数称为这个数列的第 n 项 . n 为项的序号 .Ⅱ. 注重联系,理解概念非空、每个、唯一数列实质是函数这个 “对应关系f” 是函数吗?为什么?函数111定义域 R 或 R 的子集 解析式表示法 图象 离散或连续的点的集合二、数列的本质:函 数 数列1,2,3,,Nn或它的有限子集 ,yfxxA解析式法、列表法、图象法 通项公式法、列表法、图象法一些离散的点的集合 naf n称为数列的通项公式通项公式离散函数( 特殊的函数 ) 三、数列的通项公式及应用例 1. 根据下面数列{an} 的通项公式,写出前 5项: 1234514,7,10,13,16aaaaa解: 1234521,2,3,4,5aaaaa通项:通通的、所有的项根据通项公式可以求任意项,判断某数是否为数列中的项.通项公式不唯一,也可能没有变式①、②用观察归纳法写出数列的一个通项公式(1)1,4,9,16,… ,变式: 2,5,10,17,… , (2)8,8,8,8 ,…,(3)(4)10,100,1000,10000, … ,变式① : 9,99,999,9999, … ,变式②: 5,55,555,5555, … ,例 2 :写出下面数列的一个通项公式,使它的前4 项分别是下列各数 3795,1,,,,210 171 1 11,,,,,2 3 4 求通项公式的方法多样1. 分析项与项的序号 n 的关系2. 注意各项符号特征,如果是分数还要注意分别观察分子、分母的特征;4. 积累常见数列:奇数数列、偶数数列、平方数列、99 数列、 倒数数列、符号数列的通项公式5. 分析数列与常见数列的关系Ⅲ. 深层理解,研究性质问题 . 函数的性质有哪些?数列我...