上学期北京市清华附中高一数学实数与向量的积一 课件VIP免费

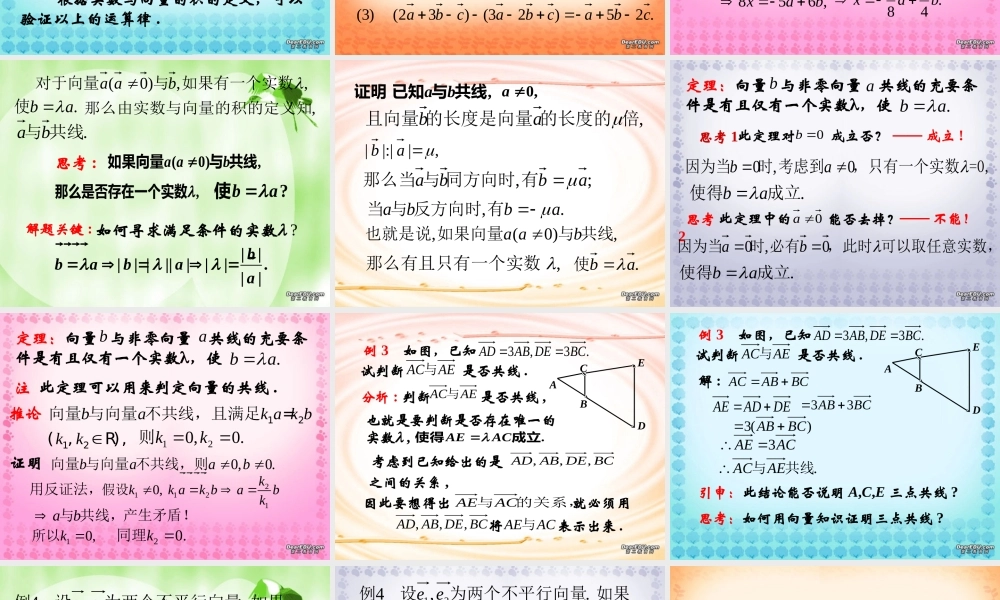
,OCOAABBCaaa uuuruuuruuuruuurrrraaaa3记作把3 .OCa�即3,aarr的方向与 的方向相同.||3|3|,33aaaa即倍的长度的的长度是 数的运算a + a + a =3a类比3aaOCa��比较两个向量与（即与 ）aarOAarBarC,.aaaa引例1:已知非零向量请作出),()()(aaaMNQMPQPN3 .PNa�即,3的方向相反的方向与aa.||3|3|,33aaaa即倍的长度的的长度是,()()().aaaa  引例2:已知非零向量请作出)()(3aaaa  把(-)记作- 类比aaa��比较两个向量-3 与-（即PN与- ）aaNaMQaP 数的运算(a)+(a)+(a)= 3a实数与向量的积定义 : aaa <0 时 , 与 反向； aaaa其中 >0 时 , 与 同向 ; aaaa=0 时 ,00a1. 实数与向量的积注 1 实数与向量的积 仍是一个向量 .a注 2 求实数与向量的积的运算叫做向量的数乘 .(1) ()() ;aa (2) ();aaa(3) ().abab��2 ．运算律：设 为任意向量 , ,  为任意实数 , 则 根据实数与向量的积的定义，可以验证以上的运算律 .,a b例 1 计算：).23()32( )3(;)(2)(3 )2(;4)3( )1(cbacbaababaa口答 :;124)3( )1(aa(2) 3()2()5 ;ababab.25)23()32( )3(cbacbacba例 2 设x 是未知向量，解方程.0)2(3)(5bxax 分析：本题中所求的未知量是一个向量，所以本题属于解向量方程的问题，向量方程的解法和数量方程的解法是相同的 . 解：原方程化为：,06355bxax856 ,xab.4385bax,,)0(如果有一个实数与对于向量baa.ba使,那么由实数与向量的积的定义知.共线与ba|||| ||||||.||bbabaa思考 :(0),a ab如果向量与 共线,那么是否存在一个实数?ba使如何寻求满足条件的实数 ?解题关键 :,ab证明 已知 与 共线0,a ,倍的长度的的长度是向量且向量ab,||:||ab;,abba有同方向时与那么当,.abba当 与 反方向时 有,(0),a ab...