数学 第三章 不等式 3.5.2 简单的线性规划课件1 新人教B版必修5 课件VIP免费

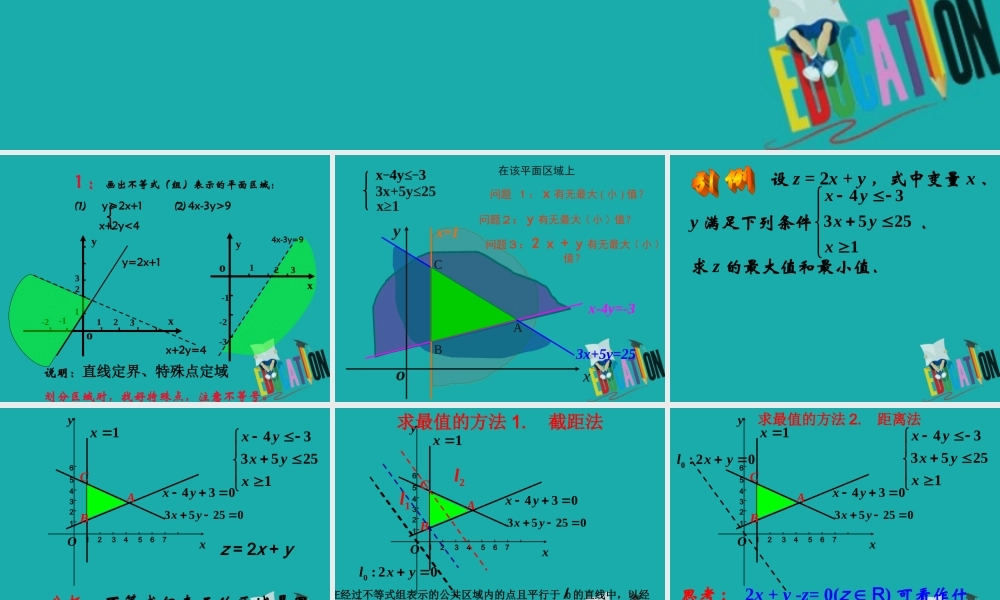
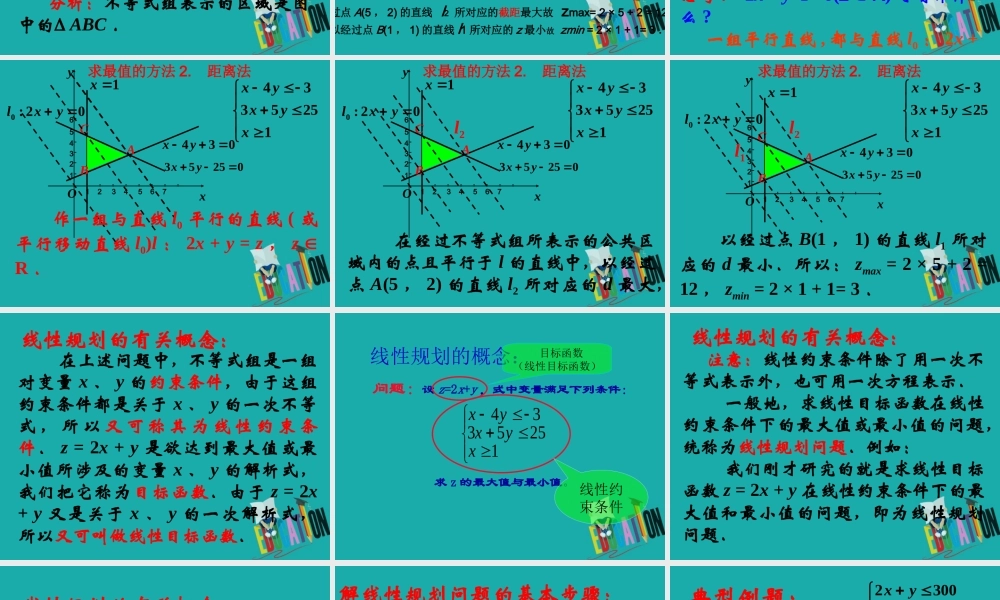
3.5.2 简单线性规划1 ：画出不等式（组）表示的平面区域：⑴ y≥2x+1 ⑵ 4x-3y>9 x+2y<4说明：直线定界、特殊点定域划分区域时，找好特殊点，注意不等号。y=2x+1x+2y=4o-1yx112233-2xo123-1-2-3y4x-3y=93x+5y≤25x-4y≤-3x≥1在该平面区域上 问题 1 ：ｘ有无最大 ( 小 ) 值？问题２：ｙ有无最大 ( 小 ) 值？xyox-4y=-33x+5y=25x=1问题３： 2 ｘ + ｙ有无最大 ( 小 )值？CAB 设 z = 2x + y ，式中变量 x 、y 满足下列条件 ．求 z 的最大值和最小值．4335251xyxyxxyO1 2 3 4 5 6 7654321034yx02553 yx1xABC 分析：不等式组表示的区域是图中的 ABC ．4335251xyxyxz = 2x + yxyO1 2 3 4 5 6 7654321034yx02553 yx1xABC0 : 20lxyl2l1求最值的方法 1. 截距法 在经过不等式组表示的公共区域内的点且平行于 l0 的直线中，以经过点 A(5 ， 2) 的直线 l2 所对应的截距最大故 zmax= 2 × 5 + 2 = 12 ，以经过点 B(1 ， 1) 的直线 l1 所对应的 z 最小故 zmin = 2 × 1 + 1= 3 ．xyO1 2 3 4 5 6 7654321034yx02553 yx1xABC0 : 20lxy4335251xyxyx思考 : 2x + y -z= 0(z  R) 可看作什么 ? 一组平行直线 , 都与直线 l0 ： 2x + y = 0 平行 .求最值的方法 2. 距离法 xyO1 2 3 4 5 6 7654321034yx02553 yx1xABC0 : 20lxy4335251xyxyx 作一组与直线 l0 平行的直线 ( 或平行移动直线 l0)l ： 2x + y = z ， z  R ． 求最值的方法 2. 距离法 xyO1 2 3 4 5 6 7654321034yx02553 yx1xABC0 : 20lxy4335251xyxyx 在经过不等式组所表示的公共区域内的点且平行于 l 的直线中，以经过点 A(5 ， 2) 的直线 l2 所对应的 d 最大，l2求最值的方法 2. 距离法 4335251xyxyx 以经过点 B(1 ， 1) 的直线 l1 所对应的 d 最小．所以： zmax = 2 × 5 + 2 = 12 ， zmin = 2 × 1 + 1= 3 ．xyO1 2 3 4 5 6 7654321034yx02553 yx1xABC0 : 20lxyl2l1求最值的方法 2. 距离法 在上述问题中，不...