数学 1.1.2 余弦定理课件1 新人教A版必修5 课件VIP免费

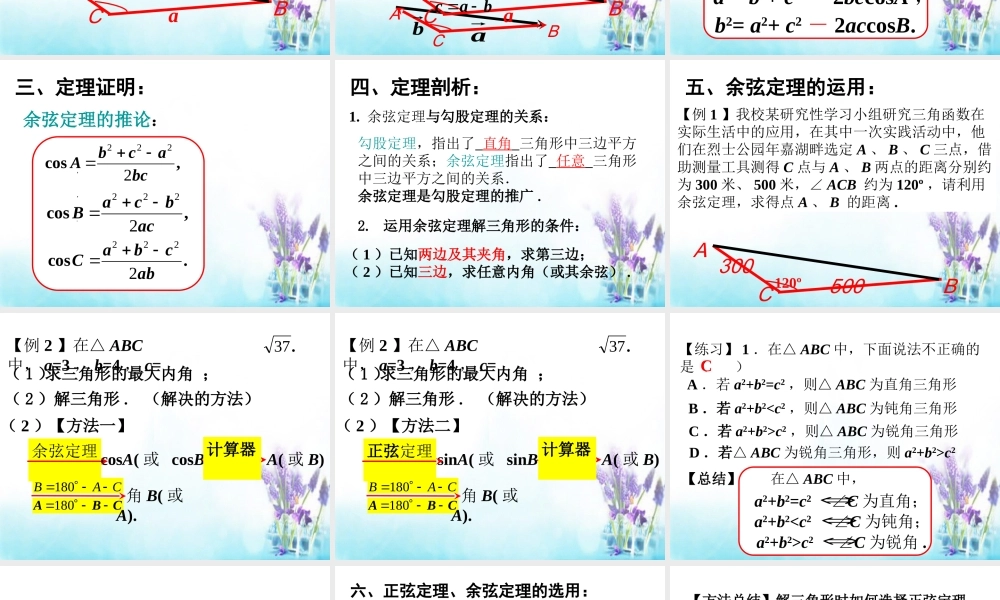
1.1.2 余弦定理一、复习回顾：1. 正弦定理：.sinsinsinCcBbAa中，ABC2. 运用正弦定理解三角形的条件：① 已知 ，解三角形．② 已知 ，解三角形．两角及任意一边两边及其中一边的对角二、课题引入——实际情景：我校某研究性学习小组研究三角函数在实际生活中的应用，在其中一次实践活动中，他们在烈士公园年嘉湖畔选定 A 、 B 、 C 三点，借助测量工具测得 C 点与 A 、 B 两点的距离分别约为 300 米、500 米，∠ ACB 约为 120º ，他们将利用数学知识，求得两点 A 、 B 之间的距离 .CB300500A120ºΔABC 中， AC=300 ， BC=500 ，∠ ACB =120º ，求 AB 长 .问题：在已知三角形 ΔABC 的两边 a 、 b及其夹角 C 的条件下，能否利用已学的正弦定理解出三角形呢？二、课题引入——数学问题：CB300500A120º1.2.1 余弦定理AbaCBcΔABC 中，已知 a ， b ，及∠ C ，求 c边 .三、定理探索及证明：如图，设=a2+ b2 － 2abcosC .,,,cABbCAaCB,bac那么)()(||2babacccbabbaa2∴c2= a2+ b2 － 2abcosC .ABaCAbaCBcbacc2= a2+ b2 － 2abcosC ，三、定理证明：余弦定理：三角形任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍 .即：在 ΔABC 中，a2= b2+ c2 － 2bccosA ，b2= a2+ c2 － 2accosB.余弦定理的推论： ，，.,cosbcacbA2222三、定理证明：,cosacbcaB2222.cosabcbaC2222四、定理剖析：2. 运用余弦定理解三角形的条件： 1. 余弦定理与勾股定理的关系：勾股定理，指出了 直角 三角形中三边平方之间的关系；余弦定理指出了 任意 三角形中三边平方之间的关系．余弦定理是勾股定理的推广 .（ 1 ）已知两边及其夹角，求第三边；（ 2 ）已知三边，求任意内角（或其余弦） .五、余弦定理的运用：A 300500CB120º【例 1 】我校某研究性学习小组研究三角函数在实际生活中的应用，在其中一次实践活动中，他们在烈士公园年嘉湖畔选定 A 、 B 、 C 三点，借助测量工具测得 C 点与 A 、 B 两点的距离分别约为 300 米、 500 米，∠ ACB 约为 120º ，请利用余弦定理，求得点 A 、 B 的距离 .（ 1 ） ； 【例 2 】在△ ABC中， a=3 ， b=4 ， c=求三角形的最大内角.37（ 2 ）解三角形 . （解决的方法）（ 2 ）【方法一】...