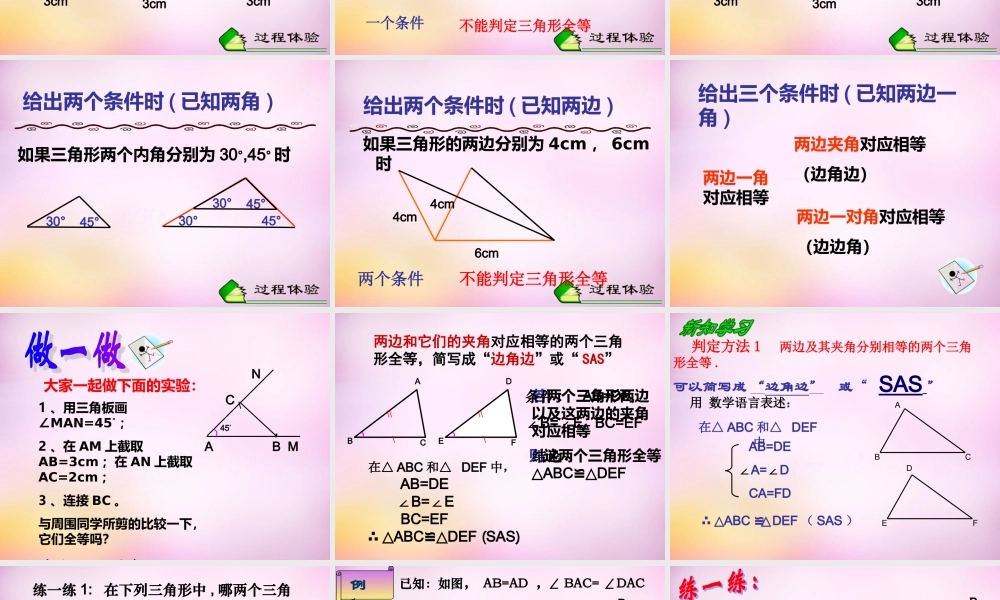
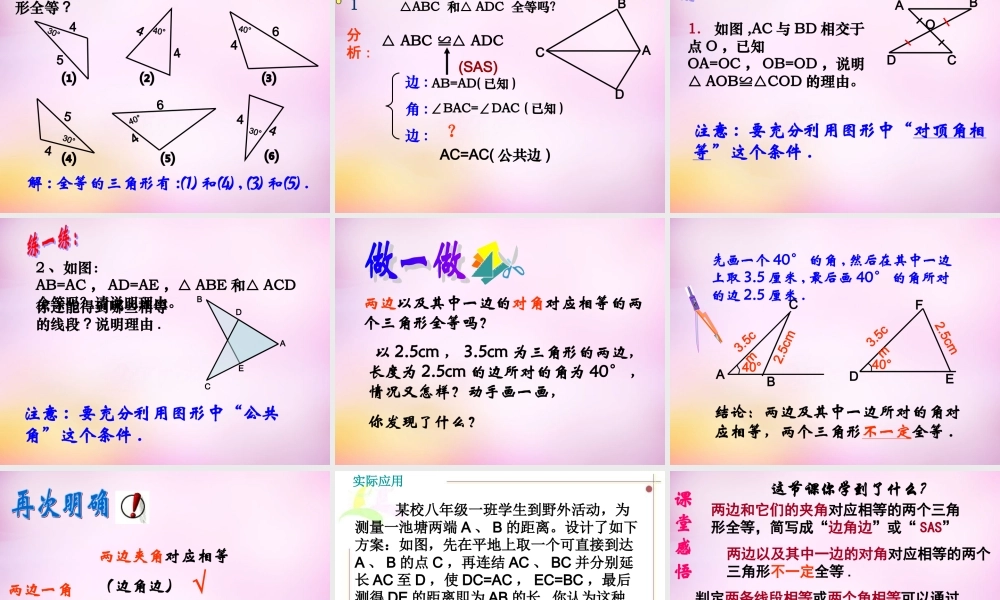
教学目标• 1. 知道三角形全等“边角边”的内容;• 2. 会运用“ S A S” 识别三角形全等,为证明线段相等或角相等创造条件;• 3. 经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。ABC已知: △ ABC DEF≌ △找出其中相等的边和角反之,判别两个三角形全等需要哪些条件?DEFAB=DE,BC=EF,CA=FD∠ A= ∠ D, ∠ B= ∠ E, ∠ C= ∠ F△ABC DEF≌ △一个条件寻求判别三角形全等的条件三个条件边边边角角角两角一边两边一角两个条件全等三角形:三组边对应相等,三对角对应相等一组边相等一对角相等两边和它的夹角两边和它一边的对角两角和它的夹边两角和一角的对边一边一角相等两对角相等两组边相等只给一个条件(一条边或一个角)只给一条边时如:3cm3cm3cm只给一个角时如:45°45°45°只给一个条件(一条边或一个角)一个条件不能判定三角形全等如果三角形的一条边为 3cm, 一个内角为 30°3cm3cm3cm30°30°30°给出两个条件时 ( 一边及一角 )给出两个条件时 ( 已知两角 )如果三角形两个内角分别为 30°,45° 时30°45°30°45°30°45°给出两个条件时 ( 已知两边 )如果三角形的两边分别为 4cm , 6cm 时6cm4cm4cm两个条件不能判定三角形全等两边一角对应相等两边夹角对应相等(边角边) 两边一对角对应相等(边边角)给出三个条件时 ( 已知两边一角 )大家一起做下面的实验:1 、用三角板画∠MAN=45° ;2 、在 AM 上截取AB=3cm ;在 AN 上截取AC=2cm ;3 、连接 BC 。与周围同学所剪的比较一下,它们全等吗?你得出什么结论?BCAMN45°′\两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“ SAS”\\\ABC\\\DEF在△ ABC 和△ DEF 中, AB=DE ∠B=E∠ BC=EF ∴ △ABCDEF ≌△(SAS) 若两个三角形两边以及这两边的夹角对应相等则这两个三角形全等条件 : AB=DE,∠B=E, BC=EF∠结论 : ABCDEF△≌△ 判定方法 1 两边及其夹角分别相等的两个三角形全等 .可以简写成 “边角边” 或“ SAS ” ABCDEF用 数学语言表述:在△ ABC 和△ DEF中 ∴ △ABC DEF≌△( SAS ) AB=DE ∠A=∠D CA=FD 练一练 1: 在下列三角形中 , 哪两个三角形全等 ?40°4430° 444530°4530°4640°4640°⑴⑵⑶⑷⑸⑹解 : 全等的三角形有 :⑴ 和⑷ , ⑶ 和⑸ .已知:如图, AB=AD ,∠ BAC= ∠DAC△ABC 和△ ADC 全...