九年级数学上册 2413 弧，弦，圆心角市级公开课课件 人教新课标版 课件VIP免费

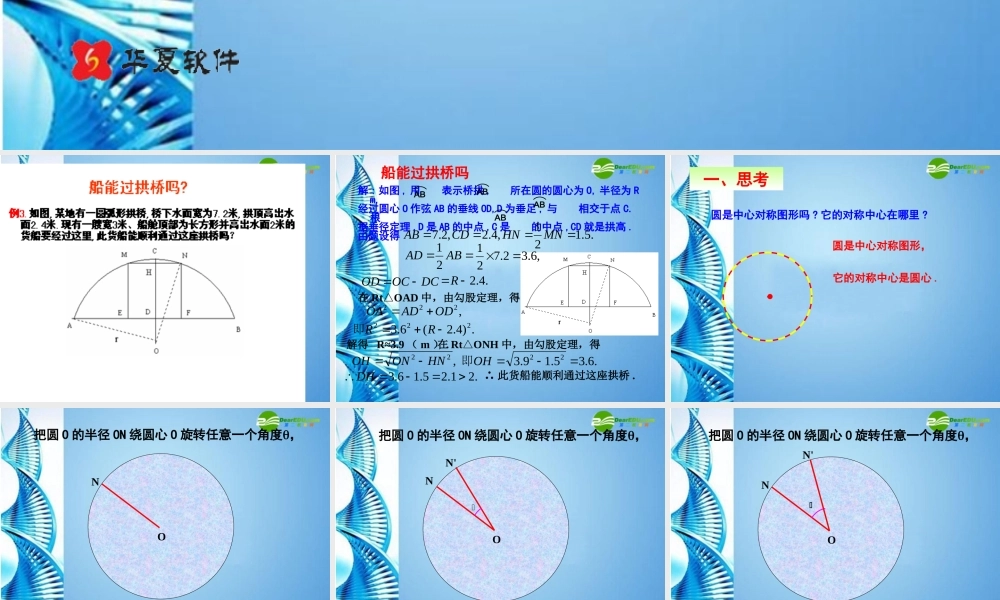
船能过拱桥吗解 : 如图 , 用 表示桥拱 , 所在圆的圆心为 O, 半径为 Rm,经过圆心 O 作弦 AB 的垂线 OD,D 为垂足 , 与 相交于点 C.根据垂径定理 ,D 是 AB 的中点 ,C 是 的中点 ,CD 就是拱高 .由题设得ABABABAB.5.121,4.2,2.7MNHNCDABABAD21,6.32.721DCOCOD.4.2R在 RtOAD△中，由勾股定理，得,222ODADOA.)4.2(6.3222RR即解得 R≈3.9 （ m ） .在 RtONH△中，由勾股定理，得,22HNONOH.6.35.19.322OH即.21.25.16.3DH∴ 此货船能顺利通过这座拱桥 . 圆是中心对称图形吗 ? 它的对称中心在哪里 ?·一、思考圆是中心对称图形，它的对称中心是圆心 . NO把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度， NON'把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度， NON'把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度， NON'把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度， NON'定理：把圆绕圆心旋转任意一个角度后，仍与原来的圆重合。把圆 O 的半径 ON 绕圆心 O 旋转任意一个角度，由此可以看出，点 N' 仍落在圆上。 · 圆心角：我们把顶点在圆心的角叫做圆心角 .OBA二、概念如图中所示， ∠ AOB 就是一个圆心角。 如图，将圆心角∠ AOB 绕圆心 O 旋转到∠ A’OB’ 的位置，你能发现哪些等量关系？为什么？根据旋转的性质，将圆心角∠ AOB 绕圆心 O 旋转到∠ A′OB′ 的位置时，显然∠ AOB ＝∠ A′OB′ ，射线 OA 与 OA′ 重合， OB 与 OB′ 重合．而同圆的半径相等， OA=OA′ ， OB=OB′ ，从而点 A 与 A′ 重合， B 与 B′ 重合．·OAB·OABA′B′A′B′三、探究''.ABA B因此，弧 AB 与弧 A1B1 重合， AB 与 A′B′ 重合．⌒AB⌒A1B1= 同样，还可以得到：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角 _____ ， 所对的弦 ________ ；在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角 ______ ，所对的弧 _________ ．这样，我们就得到下面的定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．相等相等相等相等同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．四、定理...