上学期北京市清华附中高一数学平面向量的坐标运算一 课件VIP免费

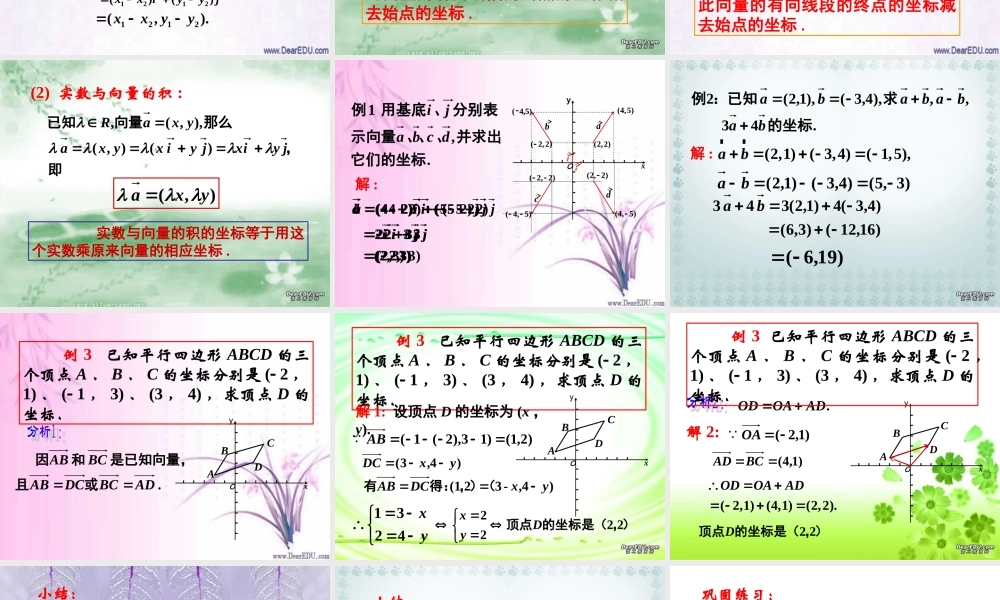
1. 平面向量基本定理的内容是什么 ? 如果 是同一平面内的两个不共线向量，那么对这一平面内的任一向量 ，有且只有一对实数 1 、 2 ，使 不共线的向量 叫做表示这一平面内所有向量的一组基底 .a12e e�、1212.aee12e e�、2. 向量共线的充要条件是什么 ?// (0).ba aba1 、平面向量的坐标表示 :oxyaijyixa (1) 怎样用坐标表示向量 a的（直角）坐标叫做向量我们把（ ), ayx记作,),( ),,(yxjyixayxa即)0,0(0 )1,0( ),0,1( jij§5.4 平面向量的坐标运算 如图所示，以原点 O 为起点与向量相等的向量为 ，则 A 点的坐标就是向量 的坐标，反之，设 ，则点 A 的坐标 (x ， y)也就是向量 的坐标 .aOA�aOAxiy j�OA�ij2 、平面向量的坐标运算 :),,(),,(:2211yxbyxa已知1122( )( )abx iy jx iy j��jyyixx)( )(21211212(,).xxyy同理可得：1122 ( )( )abx iy jx iy j��1212() ()xx iyyj�1212(,).xxyy(1) 加法与减法 :则 两个向量和与差的坐标分别等于这两个向量相应坐标的和与差 .向量加法与减法坐标运算法则： 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标 .由此可得：oxyAB),( ),(),( 12121122yyxxyxyxOAOBAB则),,(),,( 2211yxByxAAB是任意一向量，如图，设,OBOA、作向量 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标 .由此可得： 实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标 .(2) 实数与向量的积 :即，那么向量已知jyixjyixyxayxaR ) (),( ),,(,),( yxaOyxabcdij(2,2)(4,5)( 2,2)(2, 2)(4, 5)( 4, 5)( 2, 2))5,4(., 1 它们的坐标并求出、、、示向量分别表、用基底例dcbaji)3,2( 3 2 )25( )24(jijia)3,2( 3 2 )25( )24(jijib)3,2( 3 2 )25( )24(jijic)3,2( 3 2 )25( )24(jijid解 :. 43 , , ),4,3( ),1,2( 2的坐标求：已知例babababa(2,1)( 3,4)( 1,5),ab  rr)3,5()4,3()1,2( ba)16,12()3,6( )4,3(4)1,2(3 4 3ba)19,6(...