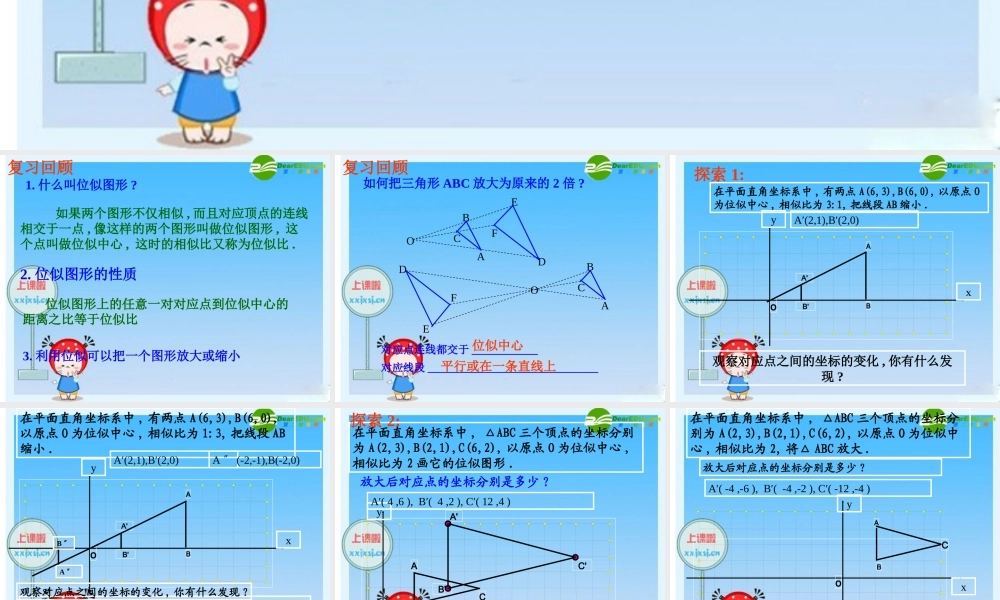
如果两个图形不仅相似 , 而且对应顶点的连线相交于一点 , 像这样的两个图形叫做位似图形 , 这个点叫做位似中心 , 这时的相似比又称为位似比 .1. 什么叫位似图形 ?2. 位似图形的性质 位似图形上的任意一对对应点到位似中心的距离之比等于位似比3. 利用位似可以把一个图形放大或缩小复习回顾DEFAOBC如何把三角形 ABC 放大为原来的 2 倍 ?DEFAOBC对应点连线都交于 ____________对应线段 _______________________________位似中心平行或在一条直线上复习回顾B'A'xyBAo在平面直角坐标系中 , 有两点 A(6,3),B(6,0), 以原点 O为位似中心 , 相似比为 3:1, 把线段 AB 缩小 .A′(2,1),B′(2,0)观察对应点之间的坐标的变化 , 你有什么发现 ?探索 1:B'A'xyBAo在平面直角坐标系中 , 有两点 A(6,3),B(6,0),以原点 O 为位似中心 , 相似比为 1:3, 把线段 AB缩小 .A′(2,1),B′(2,0)A 〞B 〞A 〞 (-2,-1),B(-2,0)在平面直角坐标系中 , 如果位似变换是以原点为位似中心 , 相似比为 k, 那么位似图形对应点的坐标的比等于 k 或 -k.观察对应点之间的坐标的变化 , 你有什么发现 ?xyo在平面直角坐标系中 , △ABC 三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2), 以原点 O 为位似中心 ,相似比为 2 画它的位似图形 .BACA′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )放大后对应点的坐标分别是多少 ?B'A'C'探索 2:还有其他办法吗 ? A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )xyo在平面直角坐标系中 , △ABC 三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2), 以原点 O 为位似中心 , 相似比为 2, 将△ ABC 放大 .A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )BAC放大后对应点的坐标分别是多少 ?xyo例题 . 在平面直角坐标系中 , 四边形 ABCD 的四个顶点的坐标分别为 A(-6,6),B(-8,2),C(-4,0),D(-2,4), 画出它的一个以原点 O 为位似中心 , 相似比为 1/2 的位似图形 .A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )BACDA′B′C′D′你还有其他办法吗 ? 试试看 .xyoB1. 如图表示△ ABC 把它缩小后得到的△ COD, 求它们的相似比ACD练一练 :xyo2. 如图△ ABC 的三个顶点坐标分别为 A(2,-2),B(4,-5),C(5,-2), 以原点 O 为位似中心 , 将这个三角形放大为原来的 2 倍 .BAC练一练 :xyo3. 如图 , 写出矩形 wxyz 各点的坐标 , 如果矩形 STUV 相似于 wxyz,点 S 的坐标为 (2,2), 按照下列相似比 , 分别写出 T 、 U 、 V 各点的坐标 . W x y z(1) 相似比为 2;(2) 相似比为 ;12练一练 :