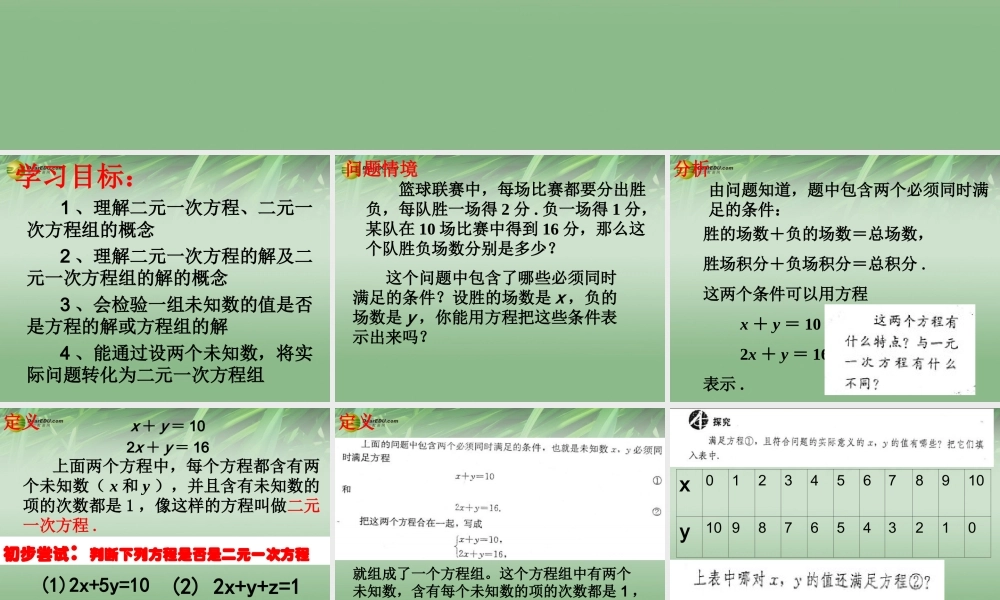
8.1 二元一次方程组学习目标: 1 、理解二元一次方程、二元一次方程组的概念 2 、理解二元一次方程的解及二元一次方程组的解的概念 3 、会检验一组未知数的值是否是方程的解或方程组的解 4 、能通过设两个未知数,将实际问题转化为二元一次方程组 篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分 . 负一场得 1 分,某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少? 这个问题中包含了哪些必须同时满足的条件?设胜的场数是 x ,负的场数是 y ,你能用方程把这些条件表示出来吗?问题情境胜的场数+负的场数=总场数,胜场积分+负场积分=总积分 .这两个条件可以用方程 x + y = 10 2x + y = 16表示 .分析由问题知道,题中包含两个必须同时满足的条件:x + y = 102x + y = 16 上面两个方程中,每个方程都含有两个未知数( x 和 y ),并且含有未知数的项的次数都是 1 ,像这样的方程叫做二元一次方程 .定义初步尝试:判断下列方程是否是二元一次方程(1)2x+5y=10(2) 2x+y+z=1(4)2x+1=0(3)x2+y=20定义就组成了一个方程组。这个方程组中有两个未知数,含有每个未知数的项的次数都是 1 ,并且一共有两个方程,像这样的方程组叫做二元一次方程组。x012345678910y10 9876543210定义• 一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解 .• 二元一次方程 3x+2y=11 ( )A 、 任何一对有理数都是它的解B 、只有一个解C 、只有两个解 D 、无穷多个解D知识巩固哪些是二元一次方程组?为什么?12)3(yxx53893)2(zyzyx05923)1(xyyx 其中( 3 )也是二元一次方程组——只要两个一次方程合起来共有两个未知数,那么他们就组成一个二元一次方程组。你猜( 2 )我们该称什么? 三元一次方程组45)4(yxyxyA. x=3y=4B.x=2y=0C.x=1y=1D. x=1y= -1探索: 不难验证:A、C是方程 (1) 的解,B、C是方程 (2) 的解,D既不是方程 (1) 的解,也不是方程 (2) 的解。只有C是两个方程的公共解。因此方程组的解是C。方程组 3 x-2y=1 (1) x + y =2 (2)的解为: ( )C挑战自己关于 x 、 y 的方程 ax2+bx+2y=3是一个二元一次方程,则 a 、 b 的值为( )A 、 a=0 且 b=0 B 、 a=0 或 b=0 C 、 a=0 且 b≠0 D 、 a≠0 且 b≠0C ...