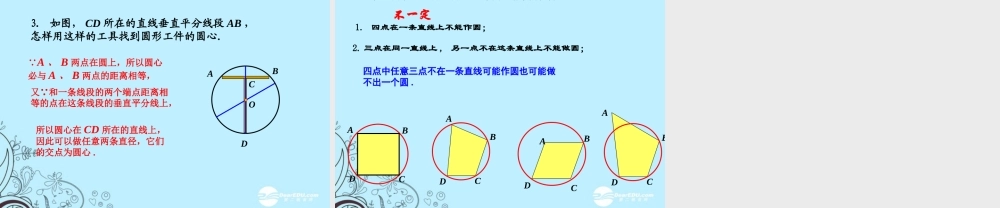
我国射击运动员在奥运会上获金牌,为我国赢得荣誉,图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗? 解决这个问题要研究点和圆的位置关系. 活 动 一r问题2:设⊙ O 半径为 r, 说出来点 A ,点 B ,点 C 与圆心 O 的距离与半径的关系:·COABOC > r.问题1:观察图中点 A ,点 B ,点 C 与圆的位置关系?点 C 在圆外 .点 A 在圆内,点 B 在圆上,OA < r ,OB = r , 活 动一:问 题 探 究设⊙ O 的半径为 r ,点 P 到圆心的距离 OP = d ,则有:点 P 在圆上 d = r ;点 P 在圆外 d > r . 点 P 在圆内 d < r ; 符号 读作“等价于”,它表示从符号 的左端可以得到右端从右端也可以得到左端. 符号 读作“等价于”,它表示从符号 的左端可以得到右端从右端也可以得到左端.r·OA问题 3 :反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?PPP 射击靶图上,有一组以靶心为圆心的大小不同的圆,他们把靶图由内到外分成几个区域,这些区域用由高到底的环数来表示,射击成绩用弹着点位置对应的环数来表示.弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击的成绩越好 .你知道击中靶上不同位置的成绩是如何计算的吗 ? 活 动 三( 1 )如图,做经过已知点 A 的圆,这样的圆你能做出多少个?( 2 )如图做经过已知点 A 、 B 的圆,这样的圆你能做出多少个?他们的圆心分布有什么特点?探究······ABA 活 动 四经过不在同一条直线上的三点做一个圆,如何确定这个圆的圆心?如图 三点 A 、 B 、 C 不在同一条直线上,因为所求的圆要经过 A 、 B 、C 三点,所以圆心到这三点的距离相等,因此这个点要在线段 AB 的垂直的平分线上,又要在线段 BC 的垂直的平分线上.不在同一条直线上的三点确定一个圆.·COABl1l23. 以点 O 为圆心, OA (或 OB 、 OC )为半径作圆,便可以作出经过 A 、 B 、 C 的圆.1. 分别连接 AB 、 BC 、 AC ;2. 分别作出线段 AB 的垂直平分线 l1和 l2,设他们的交点为 O ,则 OA=OB=OC ;由于过 A 、 B 、 C 三点的圆的圆心只能是点O ,半径等于 OA ,所以这样的圆只能有一个,即外接圆的圆心是三角...