新课标高一数学三角函数图象及性质 课件VIP免费

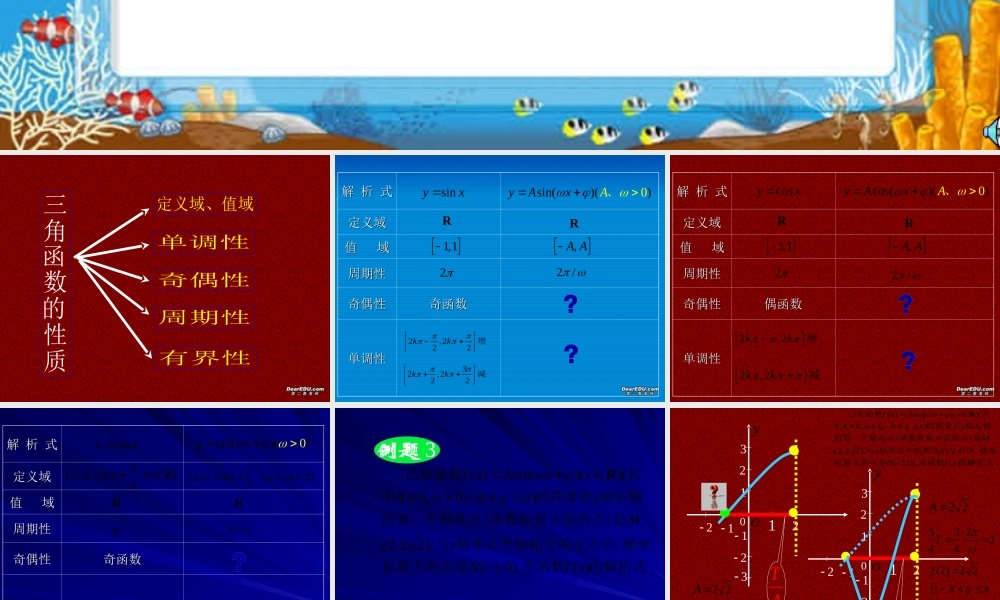
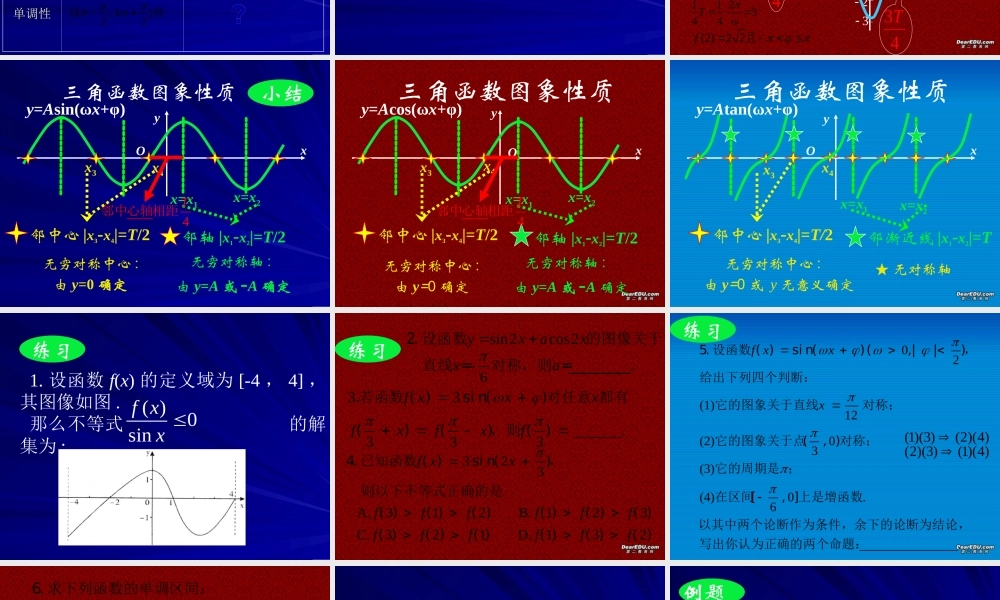
单调性定义域、值域三角函数的性质奇偶性周期性有界性解 析 式解 析 式定义域定义域值 域值 域周期性周期性奇偶性奇偶性奇函数奇函数单调性单调性sinyxsin0()()yAxA、RR1,1,A A22 / 2,222kk增32,222kk减解 析 式解 析 式定义域定义域值 域值 域周期性周期性奇偶性奇偶性偶函数偶函数单调性单调性cosyxcos0()()yAxA、RR1,1,A A22 / 2,2kk增2,2kk减 解 析 式解 析 式定义域定义域值 域值 域周期性周期性奇偶性奇偶性奇函数奇函数单调性单调性tanyxtan()()0yx { |,}2x xkkZRR/ ()22kk,增{ |()/,}2x xkkZ 2 ( )sin()()(0,0,)(2,2 2),( 1,0),( ) .f xAxxAyMxNf xR已知函数其中的图象在 轴右侧的第一个最高点(函数取最大值的点)是与 轴非正半轴相交的交点中,横坐标最大的点是求函数的解析式例题 3例题 ( )sin()()(0,0,)(2,2 2),( 1,0),( ) .f xAxxAyMxNf xR已知函数其中的图象在 轴右侧的第一个最高点(函数取最大值的点)是与 轴非正半轴相交的交点中,横坐标最大的点是求函数的解析式Oy220123123114T2 2A 11 2344T (2)2 2f且Oy2201231231134T2 2A 33 2344T (2)2 2f且 三角函数图象性质xOyx=x1x=x2x4邻中心 |x3-x4|=T/2邻轴 |x1-x2|=T/2无穷对称中心 : 由 y=0 确定 无穷对称轴 :由 y=A 或 -A 确定y=Asin(ωx+φ)x3 小结4T邻中心轴相距三角函数图象性质xOyx=x1x=x2x4邻中心 |x3-x4|=T/2邻轴 |x1-x2|=T/2无穷对称中心 : 由 y=0 确定 无穷对称轴 :由 y=A 或 -A 确定y=Acos(ωx+φ)x34T邻中心轴相距三角函数图象性质xOyx=x1x=x2x4邻中心 |x3-x4|=T/2邻渐近线 |x1-x2|=T 无穷对称中心 :由 y=0 或 y 无意义确定y=Atan(ωx+φ)x3★ 无对称轴 1. 设函数 f(x) 的定义域为 [-4 ， 4] ，其图像如图 .那么不等式 的解集为 : ( )0sinf xx 练习练习sin2cos2-.62. 设函数的图像关于 直线 =对称，则 =________yxaxxa323 A. 312 B. 123 C. 321 D. 1324....