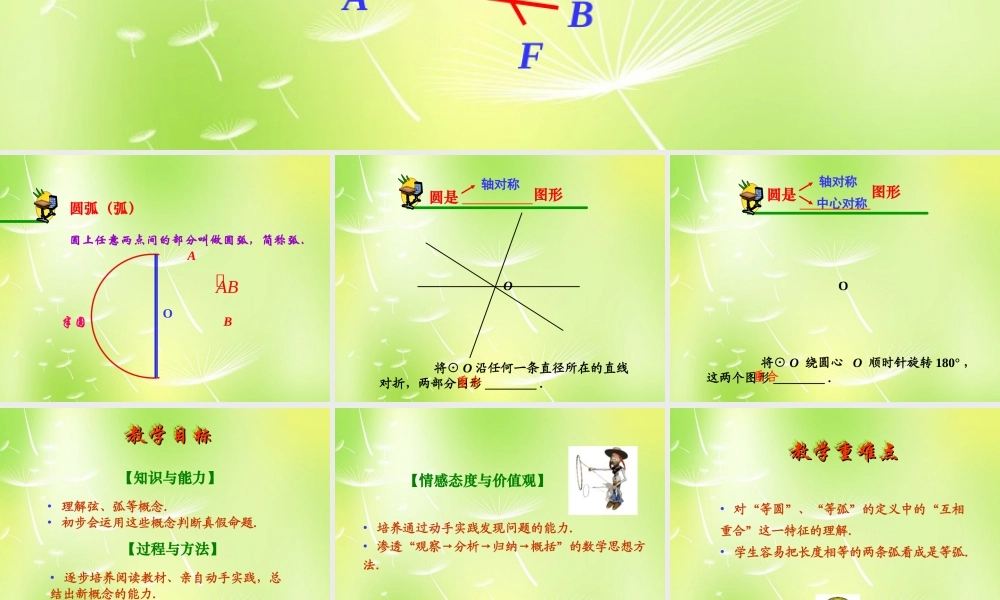
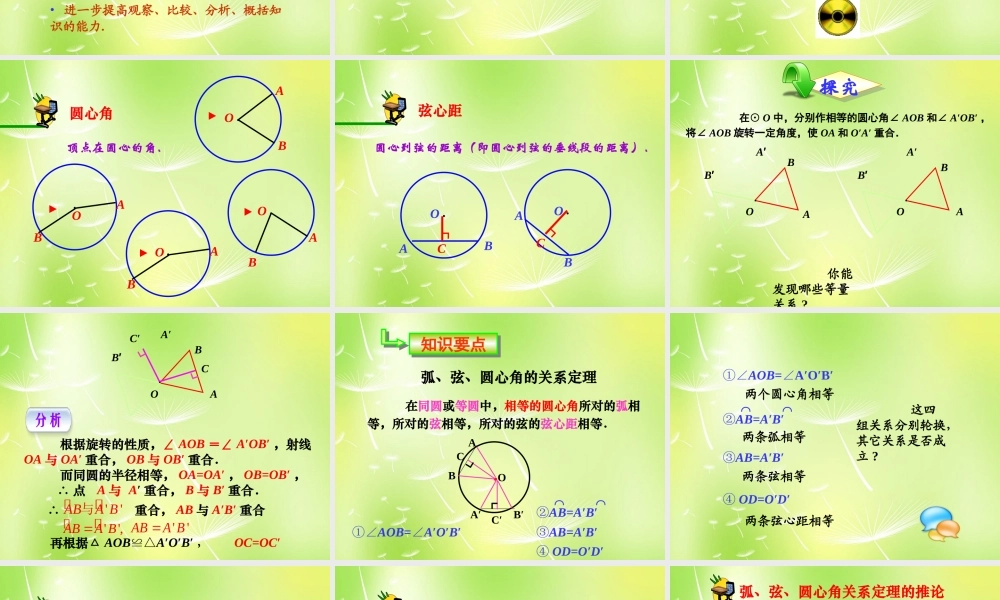
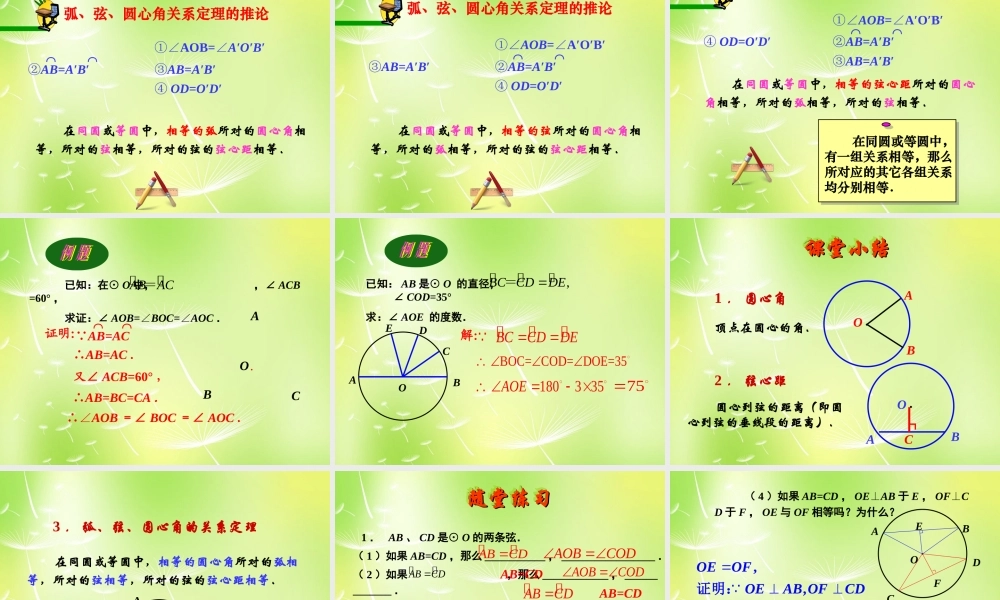
回顾旧知回顾旧知回顾旧知回顾旧知弦连接圆上任意两点的线段叫做弦.OABCDEF 圆上任意两点间的部分叫做圆弧,简称弧.圆弧(弧)OABAB半圆圆是图形轴对称___________O 将⊙ O 沿任何一条直径所在的直线对折,两部分图形 ________ .重合 将⊙ O 绕圆心 O 顺时针旋转 180° ,这两个图形 ________ .圆是图形轴对称中心对称___________O重合教学目标教学目标教学目标教学目标【知识与能力】• 理解弦、弧等概念.• 初步会运用这些概念判断真假命题.• 逐步培养阅读教材、亲自动手实践,总结出新概念的能力.• 进一步提高观察、比较、分析、概括知识的能力.【过程与方法】【情感态度与价值观】• 培养通过动手实践发现问题的能力.• 渗透“观察→分析→归纳→概括”的数学思想方法.教学重难点教学重难点教学重难点教学重难点• 对“等圆”、“等弧”的定义中的“互相重合”这一特征的理解.• 学生容易把长度相等的两条弧看成是等弧.顶点在圆心的角.·OB A圆心角·OB A·OB A·OB A圆心到弦的距离(即圆心到弦的垂线段的距离).弦心距·OB A┓C·OB A┓C 在⊙ O 中,分别作相等的圆心角∠ AOB 和∠ A′OB′ ,将∠ AOB 旋转一定角度,使 OA 和 O′A′ 重合.探究 你能发现哪些等量关系 ?·OAB·OABA′B′A′B′ 根据旋转的性质,∠ AOB =∠ A′OB′ ,射线 OA 与 OA′ 重合, OB 与 OB′ 重合. 而同圆的半径相等, OA=OA′ , OB=OB′ , ∴ 点 A 与 A′ 重合, B 与 B′ 重合.·OABA′B′'',ABA B''ABA B∴ 重合, AB 与 A′B′ 重合''ABA B与分析┓C┓C′再根据△ AOB≌△A′O′B′ ,OC=OC′ 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.●OA B┓CA′B′C′┏①∠AOB=∠A′O′B′②AB=A′B′⌒ ⌒③AB=A′B′ ④ OD=O′D′知识要点知识要点弧、弦、圆心角的关系定理①∠AOB=A′O′B′∠②AB=A′B′⌒ ⌒③AB=A′B′ ④ OD=O′D′两个圆心角相等两条弧相等两条弦相等两条弦心距相等 这四组关系分别轮换,其它关系是否成立 ?①∠AOB=∠A′O′B′②AB=A′B′⌒ ⌒③AB=A′B′ ④ OD=O′D′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等,所对的弦的弦心距相等.弧、弦、圆心角关系定理的推论①∠AOB=A′O′B′∠②AB=A′B′⌒ ⌒③AB=A...