数学 第一章 三角函数复习课教学课件 北师大版必修4 课件VIP免费

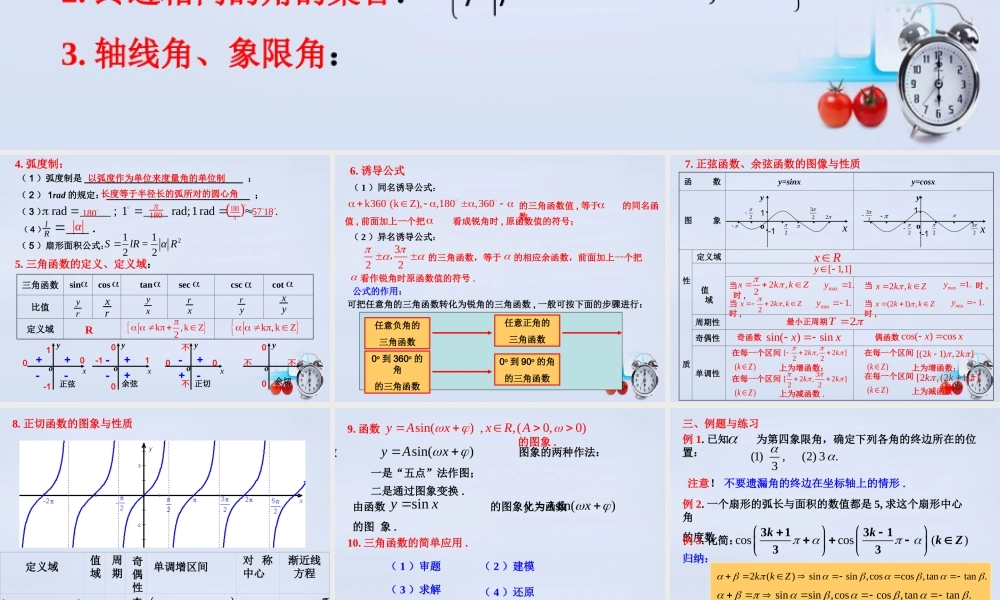
小结复习一、本章内容结构任意角的概念角度制与弧度制弧长与扇形面积公式应用任意角的三角函数计算与化简、证明恒等式应用三角函数的图象和性质诱导公式应用三角函数的简单应用二、知识要点：正角： 按逆时针方向旋转形成的角负角：按顺时针方向旋转形成的角零角： 一条射线没有作任何旋转1. 角3. 轴线角、象限角：2. 终边相同的角的集合： 360 ,ZSkk {36036090 ,Z}kkk{36090360180 ,Z}kkk{360180360270 ,Z}kkk{360270360360 ,Z}kkk（ 1 ）终边在 y 轴上的角的集合 _________________ ；（ 2 ）终边在 x 轴上的角的集合 _________________ ；（ 3 ）终边在坐标轴上的角的集合 _______________ .{90180 ,Z} nn{180 ,Z} nn{90 ,Z} nn4. 弧度制：rad_____ ; 1____ rad;1rad_____（ 1 ）弧度制是 _______________________________ ；（ 2 ） 1rad 的规定： ____________________________ ；（ 3 ）（ 4 ）___ .lR以弧度作为单位来度量角的单位制长度等于半径长的弧所对的圆心角180180π 180 π57 18α（ 5 ）扇形面积公式：21122SlR =α R5. 三角函数的定义、定义域：三角函数比值定义域sincostancotseccscyrxryxrxryxyRk,kZ2    k ,kZ   xyoxyoxyoxyo正弦010-1余弦10-10正切0不0不不0不0余切++--+--++-+-k360 (kZ),,180,360   的三角函数值 , 等于 的同名函数值 , 前面加上一个把 看成锐角时 , 原函数值的符号；6. 诱导公式（ 1 ）同名诱导公式：公式的作用：可把任意角的三角函数转化为锐角的三角函数 , 一般可按下面的步骤进行：任意负角的三角函数任意正角的三角函数0o 到 360o 的角的三角函数0o 到 90o 的角的三角函数（ 2 ）异名诱导公式：的三角函数，等于322， 的相应余函数，前面加上一个把 看作锐角时原函数值的符号 .函 数y=sinxy=cosx图 象性质定义域值 域周期性奇偶性单调性···yo···-11··22322xxR[ 1,1]y  当 时 ,2,2xkkZmax1.y当 时 ,2,2xkkZmin1.y2T最...