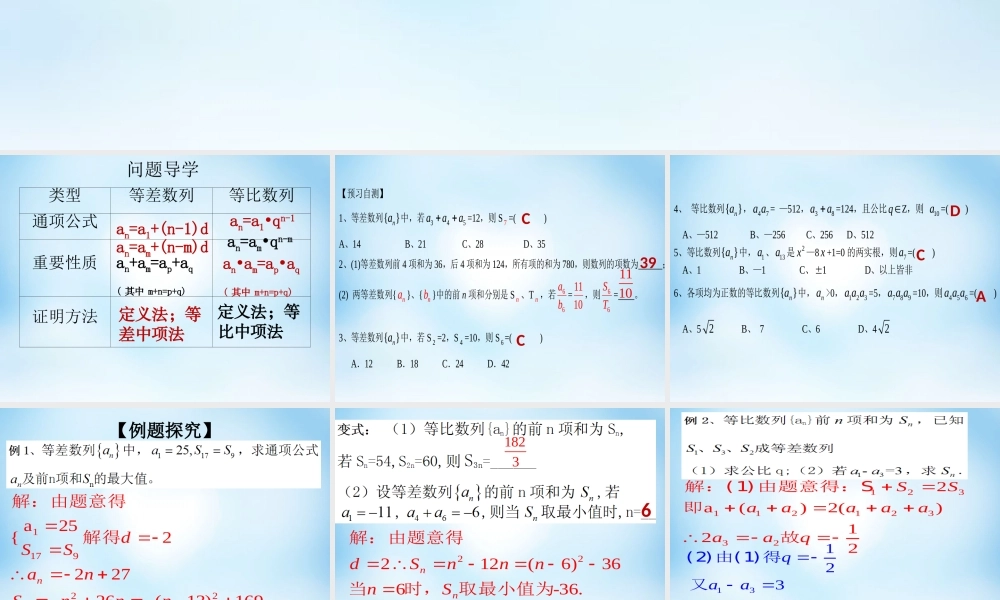
数列复习(一)问题导学类型等差数列等比数列通项公式重要性质证明方法an=a1+(n-1)dan=a1•qn-1an=am+(n-m)dan+am=ap+aq( 其中 m+n=p+q)an=am•qn-man•am=ap•aq( 其中 m+n=p+q)定义法;等差中项法定义法;等比中项法C39C【预习自测】 1、等差数列{ }na中,若345aaa=12,则 S 7 =( ) A、14 B、21 C、28 D、35 2、(1)等差数列前 4 项和为 36,后 4 项和为 124,所有项的和为 780,则数列的项数为______; (2) 两等差数列{na }、{nb }中的前 n 项和分别是 S n 、T n ,若66ab=1110,则66ST=____。 3、等差数列{ }na中,若 S 2 =2,S 4 =10,则 S 6=( ) A.12 B.18 C.24 D.42 1110CA4、 等比数列{ }na,47a a = —512,38aa=124,且公比qZ,则 10a =( ) A、—512 B、—256 C、256 D、512 5、等比数列{ }na中,1a 、13a 是2x —8 x +1=0 的两实根,则7a =( ) A、1 B、—1 C、1 D、以上皆非 6、各项均为正数的等比数列{ }na中,na >0,1 2 3a a a =5,78 9a a a =10,则4 56a a a =( ) A、5 2 B、 7 C、6 D、4 2 D【例题探究】117922a25{222726(13)16913169.nnndSSanSnnnnS解:由题意得解得当时,取最大值为1823622212(6)366-36.nndSnnnnS 解:由题意得当时,取最小值为123112123322a()2()122SSaaaaaaaq解:(1)由题意得:S即故1321111233814,[1() ]32nnqaaaa qaS(2)由(1)得又故【课后作业】1,3,916A14721、 三个数成递增的等比数列,它们的积为 27,和为 13,则这三个数依次为________________。 2、设等差数列{ }na中,S 9=72,则64aa = 。 3、等比数列{ }na中,1a =q =2,则 S5=( ) A、62 B、—62 C、30 D、66 4、由两等差数列 2,6,10,14,…,190 和 2,8,14,…,200 的公共项按从小到大顺序 组成新数列{ nc },则{nc }的各项和为__________(《必修 5》p 46 A 组第 6 题) An1256(455 ),2,()(455 )1002nnnnnnnnaaaaaaann 解:当n5时,b故S当n>5时,b故S36147118361 ,128182111(1),22211229nnnaaqaaaan解:故若则128 ()即()( )881128[1() ]2112255 (2)S