上学期北京市清华附中高一数学向量的加法与减法二 课件VIP免费

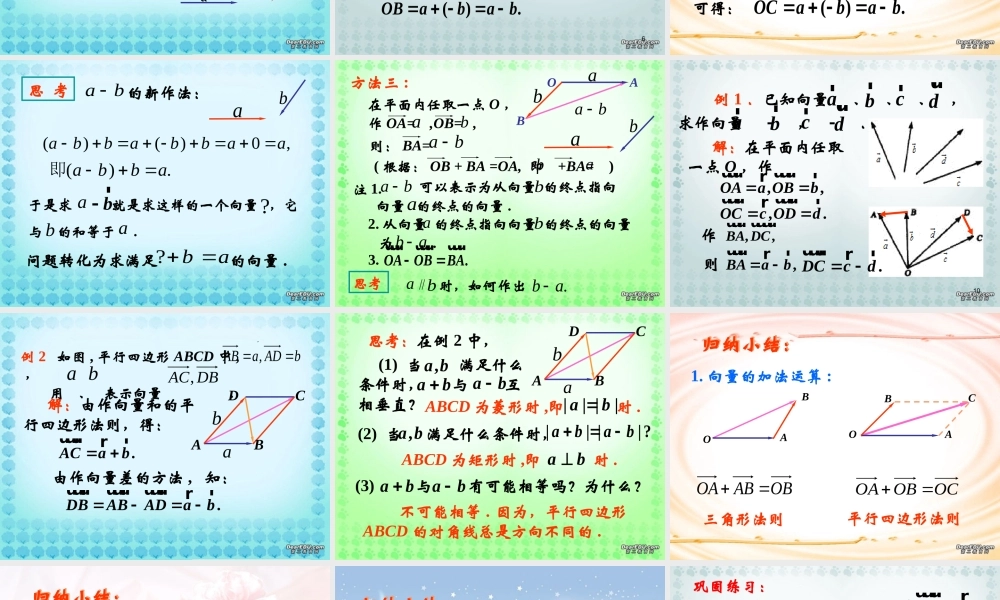
向量的减法 如图：两个人提一桶水，用力大小一样，怎样提比较省力 ?数的减法求两个数的差的运算向量的减法求两个向量差的运算类比与转化相反向量的定义两个向量差的定义向量减法的定义的定义ba )( baba的定义b的定义ba的定义b)( baba 4向量的减法 1. 相反向量： 与 长度相等，方向相反的向量叫做的相反向量 . a 记作 :.a r规定：零向量的相反向量仍是零向量 . 2) 任意向量与它的相反向量的和是零向 量 . 即 ()()0.aaaa  rrrrr,,0.ab ba abr rrrrr r 注 意1) 与 互为相反向量 . 即 aa().aa rr 3) 如果 与 互为相反向量，那么 : abar 3. 向量的减法 :().abab  rrrr即 : 2 ． 与 的差 :a b向量 加上 的相反向量，叫做 与 的差 .aba b求两个向量的差的运算叫做向量的减法 . 4 ． 的作法 :ab rab 6OA方法 一 :在平面内任取一点 O ，作 :.ABb�则由向量加法的三角形法则可得 :().OBabab   �,OAa�().abab  rrrr根据baBabab方法二 :在平面内任取一点 O ，作,.OAa OBbuuuruuurrr则由向量加法的平行四边形法则 :可得： ().OCabab   uuurrrrrabrABOCbaab于是求 就是求这样的一个向量 ，它与 的和等于 .a br?ba()()0,abbabbaa   ().abba即思 考的新作法： ba问题转化为求满足 的向量 . ab?ab2. 从向量 的终点指向向量 的终点的向量 为 .ba ab方法三 :ba则： BA=在平面内任取一点 O ，作 OA= ,OB= ,ab ( 根据： OB + BA =OA, 即 +BA= )baABObaba 可以表示为从向量 的终点指向向量 的终点的向量 .ba注 1.ba.OA OBBAuuuruuuruuur3.思考.baa b时，如何作出ab 10 例 1 ．已知向量 、 、 、 ，求作向量  ，  ．arbr 解：在平面内任取一点 O ，作,,OAa OBbuuuruuurrr作,,BA DCuuur uuuurcrdurarbrcrdur,.OCc ODduuuruuurrr,BAab uuurrr则.DCcd uuurrr 例 2 如图 , 平行四边形 ABCD 中 , ， 用 、 表示向量 .bADaAB...