上学期北京市清华附中高一数学解斜三角形应用举例 课件VIP免费

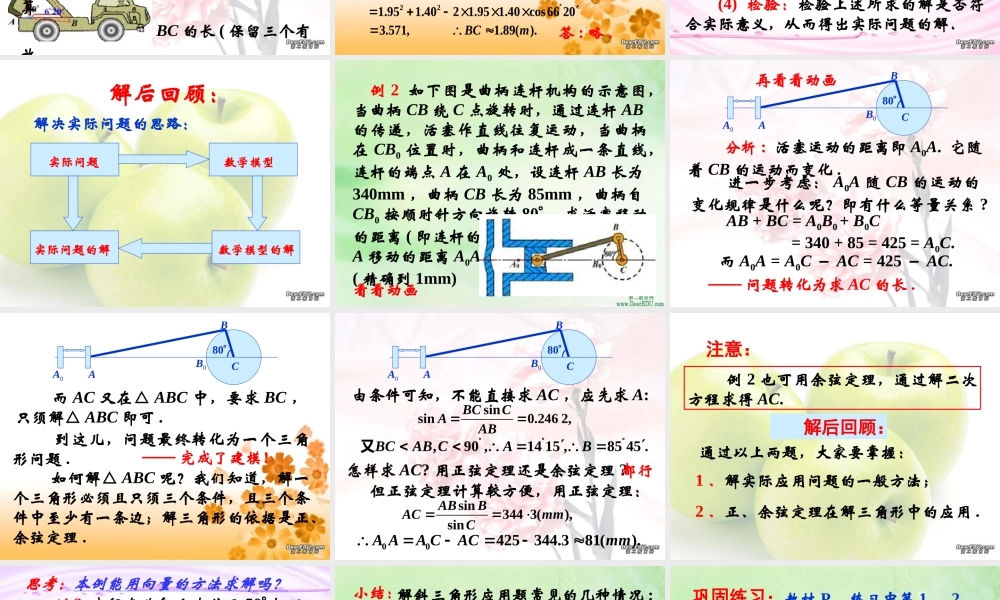
《周髀算经》是我国产生于公元前 6 、7 世纪的一部经典算书。它主要记载了有关测量的方法。当时的陈子 ( 周公后人 )被人誉为“世界测量学之祖”，《周髀算经》中记载了陈子测太阳高度的方法，大意是： 夏至时，用一长为 h 的竿子，在城南测得太阳的影子长为 a ，在相距 d 的城北测得太阳的影子长为 b(b > a) ，就可计算出太阳的高度。 夏至时，用一长为 h 的竿子，在城南测得太阳的影子长为 a ，在相距 d 的城北测得太阳的影子长为b(b > a) ，就可计算出太阳的高度。( 太阳 )OABxhabdCDEF 如图，设 AB 为 x ，则太阳高度为 x + h, 且△ ACD ∽ △DEF ．则由上式可求得 x ，从而可测得太阳高度 ..xdhba  解三角形的知识在测量、航海、几何以及物理学等方面都有非常广泛的应用，如果我们抽去每个应用题中与生产生活实际所联系的外壳，就暴露出解三角形问题的本质，这就要提高分析问题和解决问题的能力及化实际问题为抽象的数学问题的能力．下面，我们将举例来说明解斜三角形在实际中的一些应用 . 例 1 自动卸货汽车采用液压机构，设计时需要计算油泵顶杆 BC 的长度 ( 如图 ) ．已知车厢的最大仰角为 60, 油泵顶点 B 与车厢支点 A 之间的距离为 1. 95m ， AB 与水平 线之间的夹角为 620, AC 长为 1. 40m ，计算 BC 的长 ( 保留三个有效 数字 ) ．分析： (1) 什么是最大仰角？车厢立起的最大角度 .(2) 你能把问题化归为数学题吗？ 已知△ ABC 的两边 AB = 1.95m ，AC = 1.40m ，夹角 A = 6620 ，求 BC ．(3) 怎样求 BC ？用余弦定理 .2222cosBCABACAB ACA解：CAB606 201.401.95221.951.402 1.95 1.40 cos66 203.571,1.89().BCm答 : 略 .解斜三角形应用题的一般步骤是： (1) 分析：理解题意，分清已知与未知，画出示意图． (2) 建模：根据已知条件与求解目标 , 把已知量与求解量尽量集中在有关的三角形中，建立一个解斜三角形的数学模型． (3) 求解：利用正弦定理或余弦定理有序地解出三角形，求得数学模型的解． (4) 检验：检验上述所求的解是否符合实际意义，从而得出实际问题的解．解后回顾：解后回顾：解决实际问题的思路：实际问题数学模型数学模型的解实际问题的解 例 2 如下图是曲柄连杆机构的示意图，当曲柄 CB 绕 C 点旋转时，通过连杆 AB的传递...