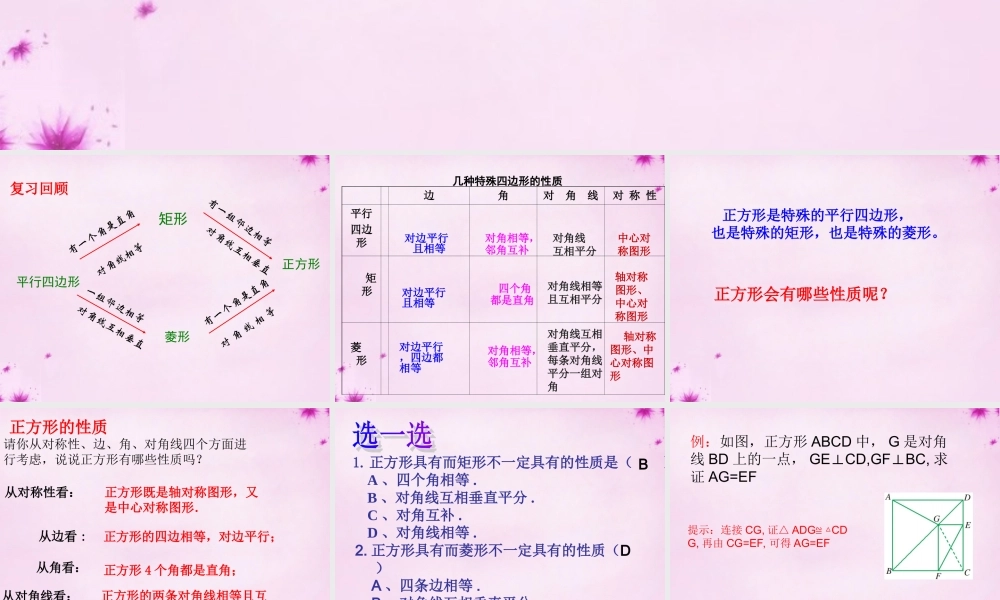
平行四边形矩形有一个角是直角正方形有一组邻边相等对角线互相垂直对角线相等菱形一组邻边相等对角线互相垂直有一个角是直角对 角 线 相 等复习回顾边角对 角 线对 称 性平行四边形 矩 形 菱 形 几种特殊四边形的性质 对边平行 且相等对边平行 且相等对边平行,四边都相等对角相等,邻角互补 四个角都是直角对角相等,邻角互补对角线互相平分对角线相等且互相平分对角线互相垂直平分,每条对角线平分一组对角中心对称图形轴对称图形、中心对称图形 轴对称图形、中心对称图形 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。 正方形会有哪些性质呢?正方形的性质请你从对称性、边、角、对角线四个方面进行考虑,说说正方形有哪些性质吗?正方形 4 个角都是直角;正方形的两条对角线相等且互相垂直平分;每一条对角线平分一组对角从角看:从对角线看:从边看 :正方形的四边相等,对边平行;从对称性看:正方形既是轴对称图形,又是中心对称图形.1.正方形具有而矩形不一定具有的性质是( ) A 、四个角相等 . B 、对角线互相垂直平分 . C 、对角互补 . D 、对角线相等 .2. 正方形具有而菱形不一定具有的性质( ) A 、四条边相等 . B 、对角线互相垂直平分 . C 、对角线平分一组对角 . D 、对角线相等 .BD例:如图,正方形 ABCD 中, G 是对角线 BD 上的一点, GECD,GFBC,⊥⊥求证 AG=EF 提示:连接 CG, 证△ ADG CD≌ △G, 再由 CG=EF, 可得 AG=EF 1. 如图,分别以△ ABC 的边 AB,AC 为一边向外画正方形 AEDB 和正方形 ACFG ,连接 CE,BG. 求证: BG=CE.证明:在正方形 ABDE 中, AE=AB ,∠ EAB=90° , 又在正方形 ACFG 中, AG=AC ,∠ GAC=90° , ∴∠ EAB=∠GAC=90°.∴∠EAC=∠GAB ,∴△ EAC≌△GAB ,∴EC=GB . ∠EAC=∠EAB+∠BAC , ∠ GAB=∠GAC+∠BAC ,课堂练习2. 正方形 ABCD 中, E 是 BC 延长线上一点,且 CE=AC, AE 交 DC 于点 F, 试求∠ E, ∠AFC 的度数解: 四边形 ABCD 为正方形,0011904522ACBBCD CE=AC ∴∠E=∠CAE ∠ACB 是⊿ ACE 的一个外角∴∠ACB=∠E+∠CAE=2∠E00114522.522EACB ∠AFC 是△ CEF 的一个外角∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°∴∠E=22.5°, ∠AFC=112.5°j FEABDC3. 已知 : 如图 , 四边...