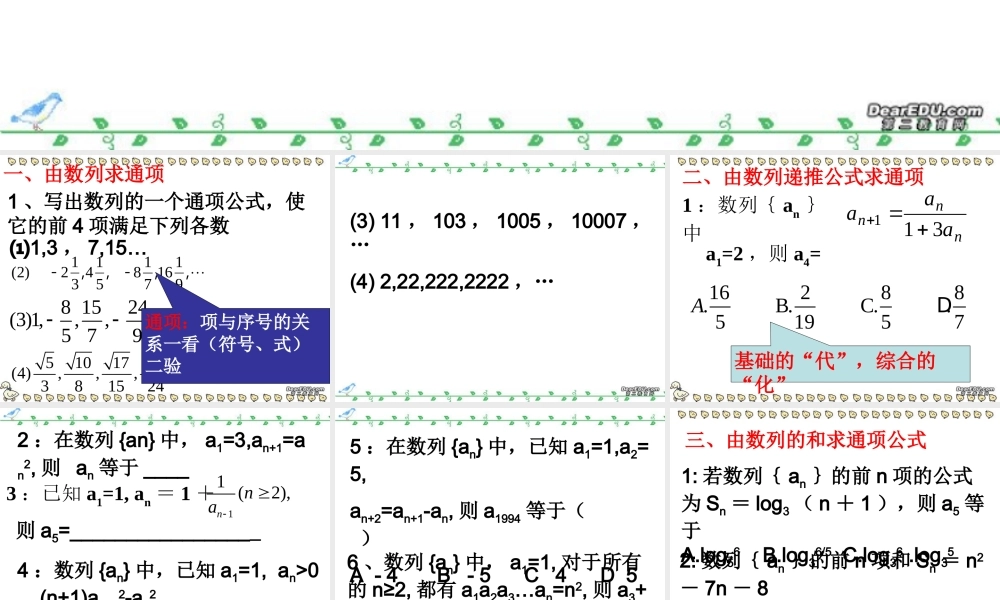
数列一1 、写出数列的一个通项公式,使它的前 4 项满足下列各数,,,-,-9116718514312)2(5101726(4),,,381524 8 1524(3)1,,,5 79⑴1,3 , 7,15… 通项:项与序号的关系一看(符号、式)二验一、由数列求通项(3) 11 , 103 , 1005 , 10007 ,…(4) 2,22,222,2222 ,…1 :数列{ an }中nnnaaa311a1=2 ,则 a4= 16288.B.C..51957A D 基础的“代”,综合的“化”二、由数列递推公式求通项2 :在数列 {an} 中, a1=3,an+1=an2, 则 an 等于 ____3 :已知 a1=1, an = 1 +4 :数列 {an} 中,已知 a1=1, an>0 (n+1)an+12-an2 +nan+1.an=0, 则 an 等于( )11 (2),nna 则 a5=________________ 6 、数列 {an} 中, a1=1, 对于所有的 n≥2, 都有 a1a2a3…an=n2, 则 a3+a5=A 61/16 B 25/9 C25/16 D31/155 :在数列 {an} 中,已知 a1=1,a2=5,an+2=an+1-an, 则 a1994 等于( )A - 4 B - 5 C 4 D 5三、由数列的和求通项公式1: 若数列{ an }的前 n 项的公式为 Sn = log3 ( n + 1 ),则 a5 等于A.log56 B.log36/5 C.log36 .log352: 数列{ an }的前 n 项和 Sn = n2- 7n - 8( 1 )求{ an }的通项公式 ⑵ 求{| an| }的前 n 项和 Tn3: 设正数数列{ an }前 n 项和为 Sn ,且存在正数 t ,使得对所有自然数n ,有 则通过归纳猜想可得到 Sn=____,2nnattS=四、项的性质函数观(定义域)1. 数列 {-2n2+29n+3} 中的最大项A 107 B 108 C 108+1/8 D 1092(*),156{}()121312 13nnnanNnaABCD变:则数列的最大项为第项第项第 、 项不存在2 、已知{ an }是递增数列,且对任意 nN*∈都有 an=n2 + λn 恒正,则实数 λ 的取值范围是A.(-7/2 , +∞) B. ( 0 ,+∞)C. (- 2 ,+∞)D. (- 3 ,+∞)A.10 B.11C.10 或 11 D.12231011nnanna、设,则数列 { }从首项到第几项的和最大五、项的单调性11111{},( , ,)nnnnnnnnnnanaaa b cnbcaaAaaBaaCaaD、已知数列的通项都是正实数 ,则与的大小关系、、、不能确定2 、 f (x) = log2x - logx4 (0 < x <1) ,又知数列{ an }的通项 an 满足 f (2an) = 2n ( nN*∈)1 )试求数列{ an }的通项表达式2 )判断数列{ an }的增减性六、综合:1 、已知数列{ an }的前 n 项和为Sn ,满足条件 lgSn +( n - 1 ) lgb = lg ( bn+1 + n - 2 ) , 其中 b> 0 ,且 b≠1( 1 )求数列{ an }的通项公式( 2 )若对 nN*, n≥4∈时,恒有 an + 1 > an ,试求 b 的取值范围