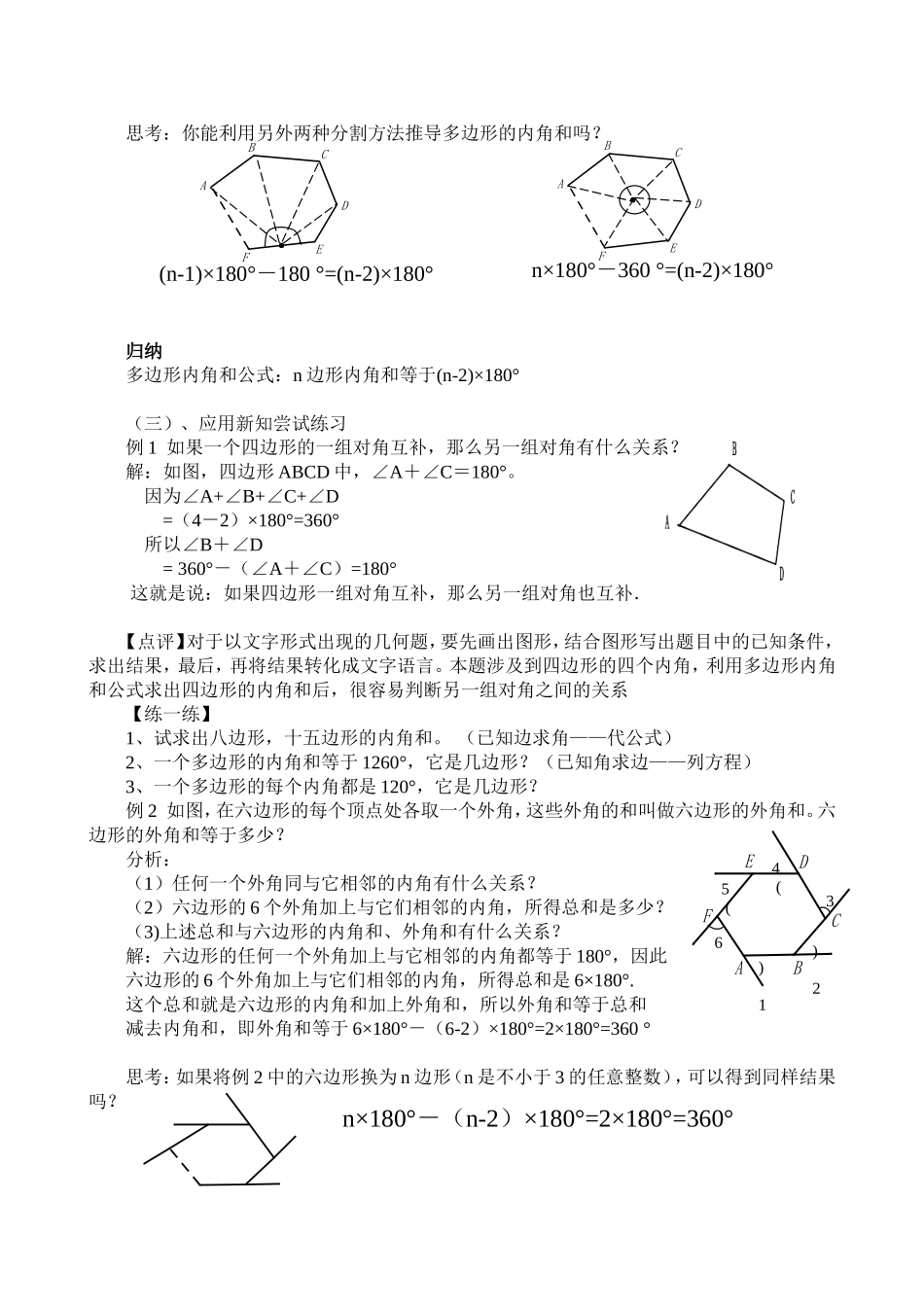
11.3.2 多边形的内角和教学目标(一)、知识目标1 理解多边形内角和公式的推导过程;2 掌握多边形内角和公式的内涵及其运用。(二)、能力目标1 通过探索多边形内角和公式培养学生类比、归纳、转化的能力;2 通过图形转化,培养学生观察分析、猜想和概括的能力。(三)、情感目标通过体会数学图形的美感,提高审美能力, 树立认识数学来源于生活,又服务于实践的观点。教学重点:探索多边形的内角和公式教学难点:如何将多边形分割成三角形,利用三角形的内角和推导多边形的内角和公式教学过程一、创设问题引入新课问题 1:前面我们已经学习了三角形的内角和,那么大家还记得三角形的内角和是多少度吗?问题 2:四边形的内角和是多少度呢?五边形呢?六边形呢?n 边形呢?二、合作交流探索新知(一)探究四边形的内角和:问题 1:长方形、正方形的内角和是多少度?问题 2:是不是任意四边形的内角和都是 360°呢?我们已经知道三角形的内角和是 180°,那么,我们能否将四边形转化成三角形,利用三角形内角和定理去求四边形的内角和?如何将四边形转化成三角形呢? 2×180=360 3×180-180=360 4×180-360=360(二)自主探究得出结论类比四边形的内角和的探究方法,你能得出五边形的内角和吗?六边形呢?……n 边形呢?(1)从五边形的一个顶点出发,可以引_______条对角线,它们将五边形分为_______个三角形,五边形的内角和等于________;(2)从六边形的一个顶点出发,可以引________条对角线,它们将六边形分为_______个三角形,六边形的内角和等于________ ; …… …… …… …… …… …… …… …… ……(3)从 n 边形的一个顶点出发,可以引________条对角线,它们将 n 边形分为_______个三角形,n 边形的内角和等于________ .思考:你能利用另外两种分割方法推导多边形的内角和吗?归纳多边形内角和公式:n 边形内角和等于(n-2)×180°(三)、应用新知尝试练习例 1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形 ABCD 中,∠A+∠C=180°。 因为∠A+∠B+∠C+∠D =(4-2)×180°=360° 所以∠B+∠D = 360°-(∠A+∠C)=180° 这就是说:如果四边形一组对角互补,那么另一组对角也互补.【点评】对于以文字形式出现的几何题,要先画出图形,结合图形写出题目中的已知条件,求出结果,最后,再将结果转化成文字语言。本题涉及到四边形的四个内角,利用多边...