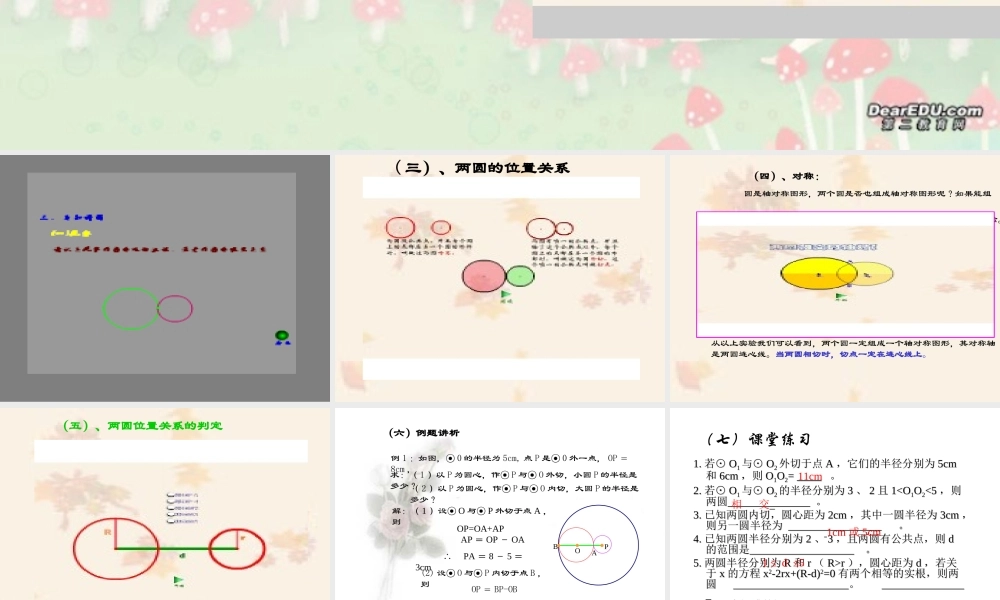
一、复习引入1 、点与圆的位置关系2 、直线与圆的位置关系3 、两个圆的位置关系 如何呢?这就是我们 这节课要解决的问题AOBCddR d( 三)、两圆的位置关系 (四)、对称: 圆是轴对称图形,两个圆是否也组成轴对称图形呢?如果能组 成轴对图形,那么对称轴是什么?我们一起来看下面的实验。 从以上实验我们可以看到,两个圆一定组成一个轴对称图形,其对称轴是两圆连心线。当两圆相切时,切点一定在连心线上。(五)、两圆位置关系的判定(六)例题讲析例 1 :如图,⊙ 0 的半径为 5cm, 点 P 是⊙ 0 外一点, OP =8cm ,求:( 1 )以 P 为圆心,作⊙ P 与⊙ O 外切,小圆 P 的半径是多少?( 2 )以 P 为圆心,作⊙ P 与⊙ O 内切,大圆 P 的半径是多少?ABPO解:( 1 )设⊙ O 与⊙ P 外切于点 A ,则 OP=OA+AP AP = OP - OA ∴ PA = 8 - 5 =3cm(2) 设⊙ O 与⊙ P 内切于点 B ,则OP = BP-OBPB = OP + OB = 8+5 =13cm1.1. 若⊙若⊙ OO11 与⊙与⊙ OO22 外切于点外切于点 AA ,它们的半径分别为,它们的半径分别为 5cm5cm和和 6cm6cm ,则,则 OO11OO22= = 。。2.2. 若⊙若⊙ OO11 与⊙与⊙ OO22 的半径分别为的半径分别为 33 、、 22 且且 1rR>r ),圆心距为),圆心距为 dd ,若关,若关于于 xx 的方程的方程 xx22-2rx+(R-d)-2rx+(R-d)22=0=0 有两个相等的实根,则两有两个相等的实根,则两圆 圆 。 。 11cm相 交 1cm 或 5cm 1 ≤ d ≤5 内切或外切。(七)课堂练习八、本讲小节1 、复习了点与圆及直线与圆的位置关系2 、学习两圆五种位置关系中两圆半径与圆心距的数量关系3 、学习两圆相切及相交时的对称性图图形形性质性质及判及判定定公共公共点个点个数数外离 d>R+r外切 d=R+r外离 R-r