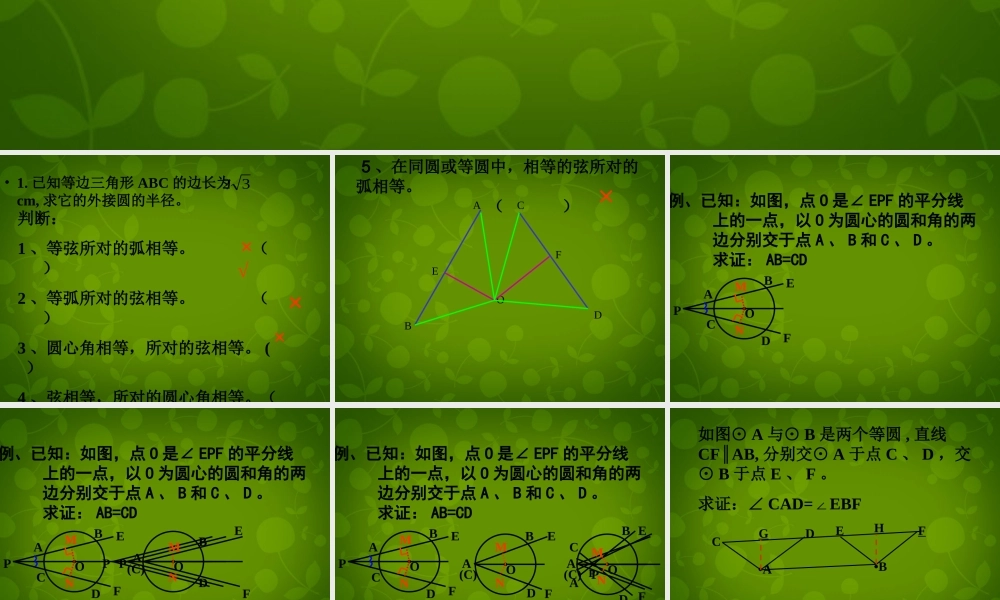
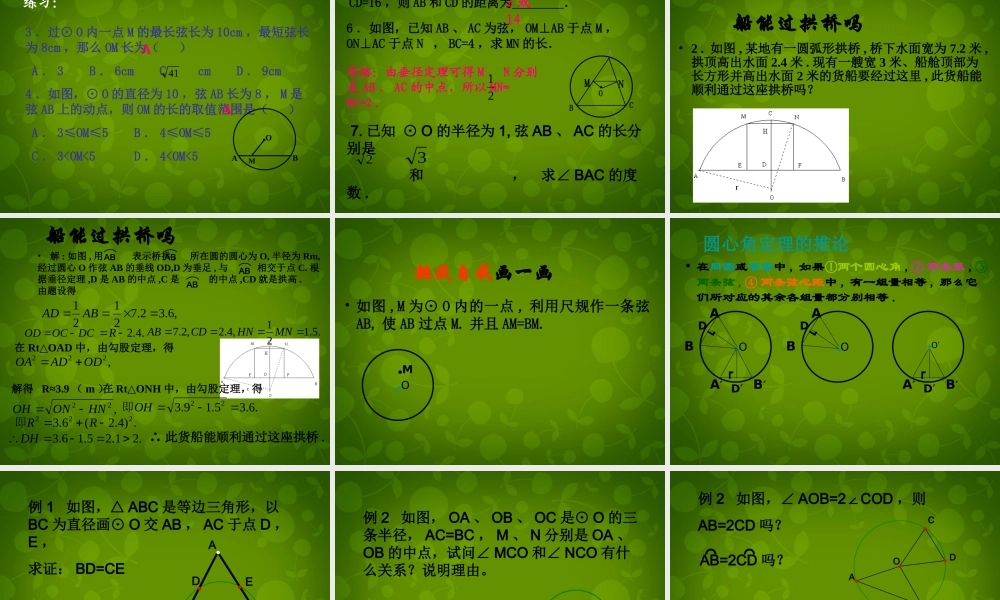
习题目标 : 熟练运用圆心角定理及其逆定理• 1. 已知等边三角形 ABC 的边长为 cm, 求它的外接圆的半径。32判断:1 、等弦所对的弧相等。 ( )2 、等弧所对的弦相等。 ( )3 、圆心角相等,所对的弦相等。 ( )4 、弦相等,所对的圆心角相等。( ) ×××√•OABCDEF5 、在同圆或等圆中,相等的弦所对的弧相等。 ( )×例、已知:如图,点 O 是∠ EPF 的平分线 上的一点,以 O 为圆心的圆和角的两 边分别交于点 A 、 B 和 C 、 D 。 求证: AB=CDPOAFEDCBMN例、已知:如图,点 O 是∠ EPF 的平分线 上的一点,以 O 为圆心的圆和角的两 边分别交于点 A 、 B 和 C 、 D 。 求证: AB=CDPOAFED(C)BPPOAFEDCBMNMN例、已知:如图,点 O 是∠ EPF 的平分线 上的一点,以 O 为圆心的圆和角的两 边分别交于点 A 、 B 和 C 、 D 。 求证: AB=CDOAFED(C)BPOAFEDCBMNOA(C)FEBPCADP思考:求证: BP=DPMNMN如图⊙ A 与⊙ B 是两个等圆 , 直线CF AB,∥分别交⊙ A 于点 C 、 D ,交⊙ B 于点 E 、 F 。求证:∠ CAD=EBF∠•A•BCDEFGH•ABCDMNO如图 M 、 N 为 AB 、 CD 的中点 , 且AB=CD.求证:∠ AMN =∠ CNM1. 已知⊙ O 的半径为 R, 弦 AB 的长也是 R, 则∠ AOB的度数是 _________.2. 圆的一条弦把圆分为 5: 1 两部分 , 如果圆的半径是2cm 则这条弦的长是 _____cm.3. 在半径为 2cm 的⊙ O 中有长为 23cm 的弦 AB, 则弦 AB 所对的圆心角的度数为 ( ) A.60° B.90° C.120° D.150° 34. 已知 : 如图 , 在⊙ O 中 , 弦 AB 的长是半径 OA 的倍 ,C 为弧AB的中点 ,AB 、 OC 相交于点 M. 试判断四边形 OACB 的形状 , 并说明理由 .MCBAOBAODBBC5. 如图 ,AB 是⊙ O 的直径 ,P 是 AB 上一点 ,C 、 D 分别是圆上的点 , 且∠ CPB=DPB,∠弧, 试比较线段 PC 、 PD 的大小关系 .6 点 A 是半圆上的三等分点 ,B 是弧 NA 的中点 ,P 是直径MN 上一动点 .O⊙的半径为 1, 问 P 在直线 MN 上什么位置时 ,AP+BP 的值最小 ? 并求出 AP+BP 的最小值 .NMBPAODCBPAO垂径定理及逆定理• 如图 , 在下列五个条件中 :只要具备其中两个条件 , 就可推出其余三个结论 .●OABCDM└⌒ ⌒⑤AD=BD. ① CD 是直径, ③ AM=BM, ② CDAB,⊥⌒...