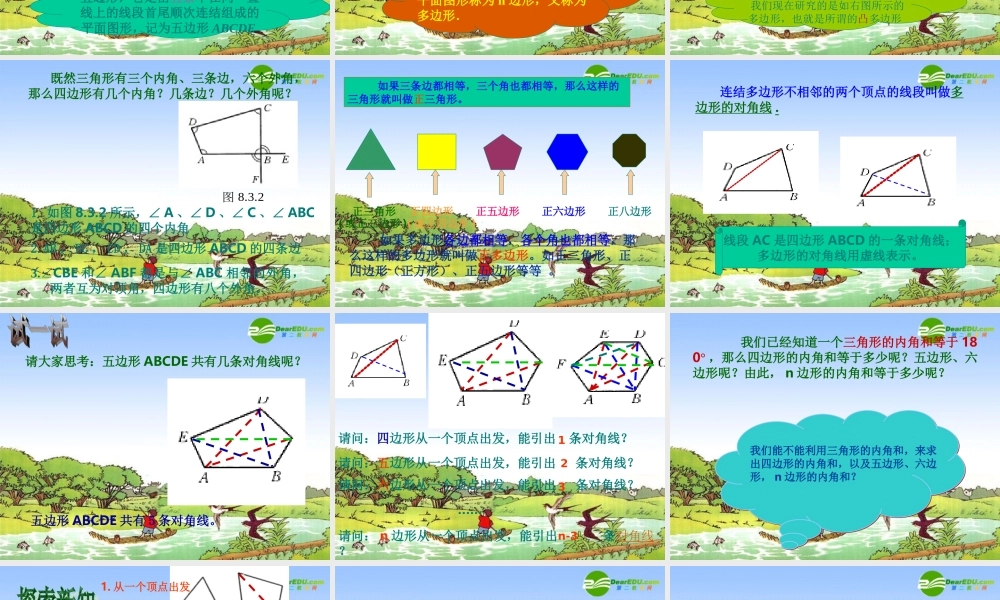
目录1. 多边形的概念2. 正多边形的概念3. 多边形的对角线4. 多边形的内角和 三角形有三个内角、三条边,我们也可以把三角形称为三边形(但我们习惯称为三角形). 你能说说什么叫做三角形吗?三角形是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形 你能根据三角形的概念,说说什么叫做四边形吗?四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形,记为四边形 ABCD 五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形,记为五边形 ABCDE 一般地,由 n 条不在同一直线上的线段首尾顺次连结组成的平面图形称为 n 边形,又称为多边形.什么叫做多边形呢? 下面所示的第一个图形也是多边形,但不在我们现在研究的范围内 。注 意我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形 有什么不同?凹多边形凸多边形 图 8.3.2 1. 如图 8.3.2 所示,∠ A 、∠ D 、∠ C 、∠ ABC是四边形 ABCD 的四个内角 3.∠CBE 和∠ ABF 都是与∠ ABC 相邻的外角, 两者互为对顶角,四边形有八个外角。 既然三角形有三个内角、三条边,六个外角,那么四边形有几个内角?几条边?几个外角呢?2.AB , BC , CD , DA 是四边形 ABCD 的四条边 如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。 如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形。如正三角形、正四边形(正方形)、正五边形等等 。正三角形正四边形正五边形正六边形正八边形( 或正三边形 )( 或正四边形 ) 连结多边形不相邻的两个顶点的线段叫做多边形的对角线 . 线段 AC 是四边形 ABCD 的一条对角线;多边形的对角线用虚线表示。 请大家思考:五边形 ABCDE 共有几条对角线呢?五边形 ABCDE 共有 5 条对角线。 请问:四边形从一个顶点出发,能引出 条对角线?请问:五边形从一个顶点出发,能引出 条对角线?请问:六边形从一个顶点出发,能引出 条对角线?请问: n 边形从一个顶点出发,能引出 条对角线? ……123n-3 我们已经知道一个三角形的内角和等于 180° ,那么四边形的内角和等于多少呢?五边形、六边形呢?由此, n 边形的内角和等于多少呢?我们能不能利用三角形的内角和,来求出四边形的内角和,以及五边形、六边形, n 边形的内角和? 请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?345n-2540...