九年级数学下册 13 解直角三角形课件1 (新版)浙教版 课件VIP免费

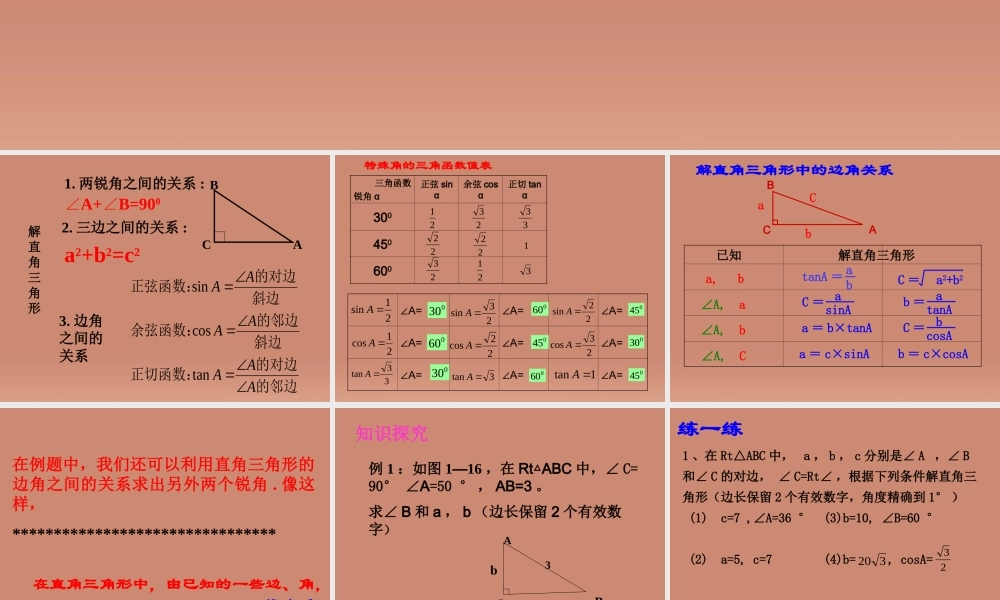
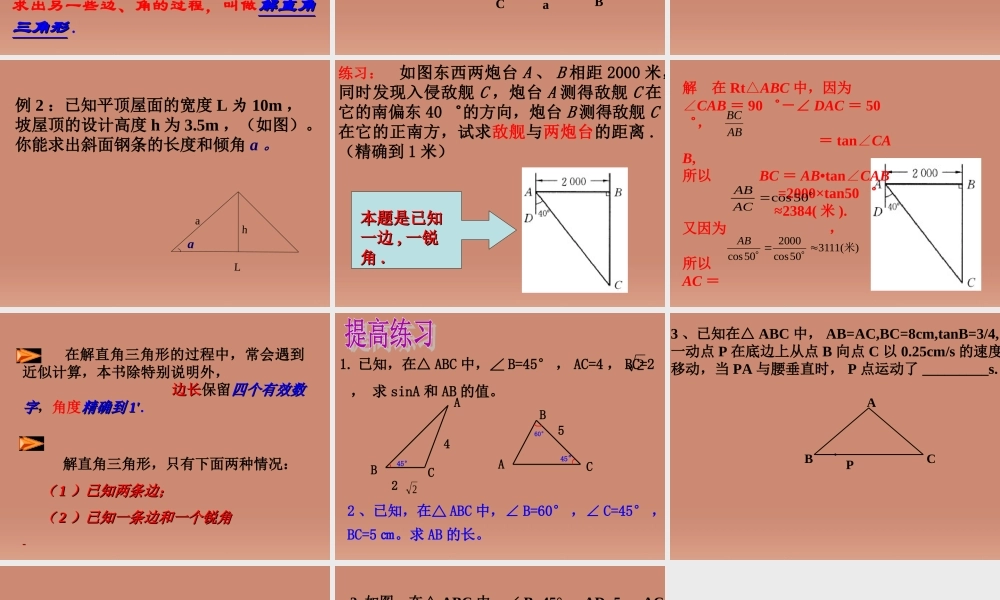
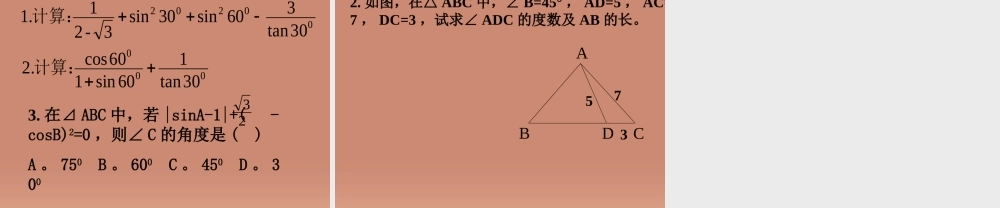
1.3 解直角三角形 (1)解直角三角形1. 两锐角之间的关系 :2. 三边之间的关系 :3. 边角之间的关系∠A+B=90∠0a2+b2=c2CAB的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin特殊角的三角函数值表三角函数锐角 α正弦 sinα余弦 cosα正切 tanα3004506002123332222123213∠A=∠A=∠A=∠A=∠A=∠A=∠A=∠A=∠A=21sinA21cosA33tanA03023sinA06022cosA0303tanA22sinA23cosA1tanA060045045030060045 已知解直角三角形a, ｂtanA ＝ ab∠A, aC ＝asinA∠A, bb ＝atanAC ＝bcosAa ＝ b×tanAC ＝ a2+b2∠A, Ca ＝ c×sinAb ＝ c×cosA解直角三角形中的边角关系CBAaｂC在例题中，我们还可以利用直角三角形的边角之间的关系求出另外两个锐角 . 像这样，******************************** 在直角三角形中，由已知的一些边、角，求出另一些边、角的过程，叫做解直角解直角三角形三角形 .例 1 ：如图 1—16 ，在 Rt ABC△中，∠ C=90° ∠A=50 ° ， AB=3 。求∠ B 和 a ， b （边长保留 2 个有效数字）3ABCab知识探究练一练1 、在 Rt△ABC 中， a ， b ， c 分别是∠ A ，∠ B和∠ C 的对边， ∠ C=Rt∠ ，根据下列条件解直角三角形（边长保留 2 个有效数字，角度精确到 1° ） (1) c=7 ,∠A=36 ° (3)b=10, ∠B=60 ° (2) a=5, c=7 (4)b= , cosA=32023例 2 ：已知平顶屋面的宽度 L 为 10m ，坡屋顶的设计高度 h 为 3.5m ，（如图）。你能求出斜面钢条的长度和倾角 a 。ahLa练习： 如图东西两炮台 A 、 B 相距 2000 米，同时发现入侵敌舰 C ，炮台 A 测得敌舰 C 在它的南偏东 40 ゜的方向，炮台 B 测得敌舰 C在它的正南方，试求敌舰与两炮台的距离 .（精确到 1 米） 本题是已知本题是已知一边一边 ,, 一锐一锐角角 .. 解 在 Rt△ABC 中，因为∠CAB ＝ 90 ゜－∠ DAC ＝ 50゜， ＝ tan∠CAB,所以 BC ＝ AB•tan∠CAB =2000×tan50 ゜ ≈2384( 米 ).又因为 ，所以 AC ＝答：敌舰与 A 、 B 两炮台的距离分别约为 3111 米和 2384 米 .ABBC50cosACAB)(311150cos200050cos米AB 在解直角三角形的过程中，常会遇到近似计算，本书除特别说明外， 边长边长保留四个有效数四个有效数字字，角度精确到精确到 1′1′. 解直角...