数学 第三章 不等式 3.5.2 简单的线性规划课件2 新人教B版必修5 课件VIP免费

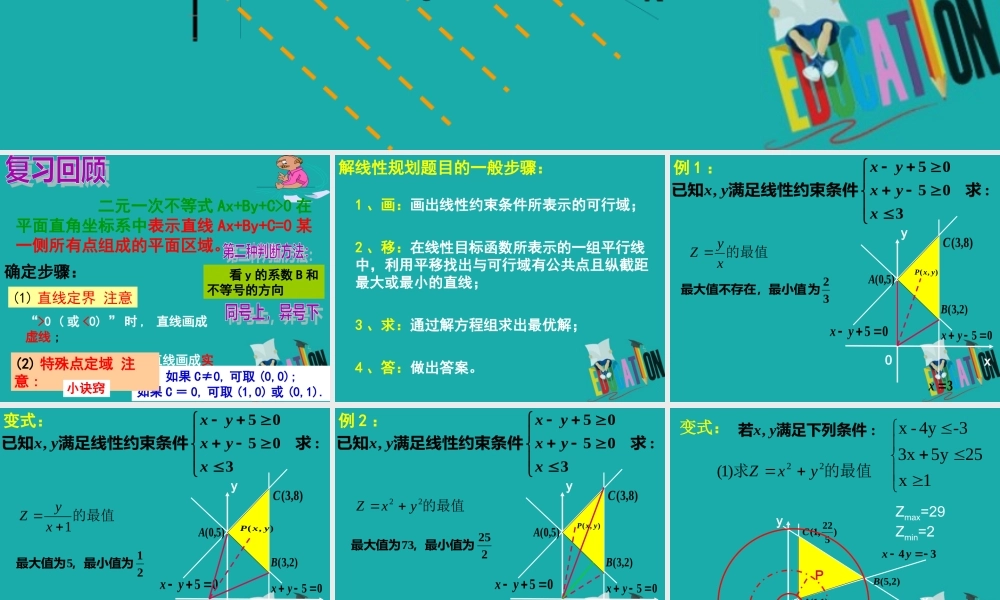
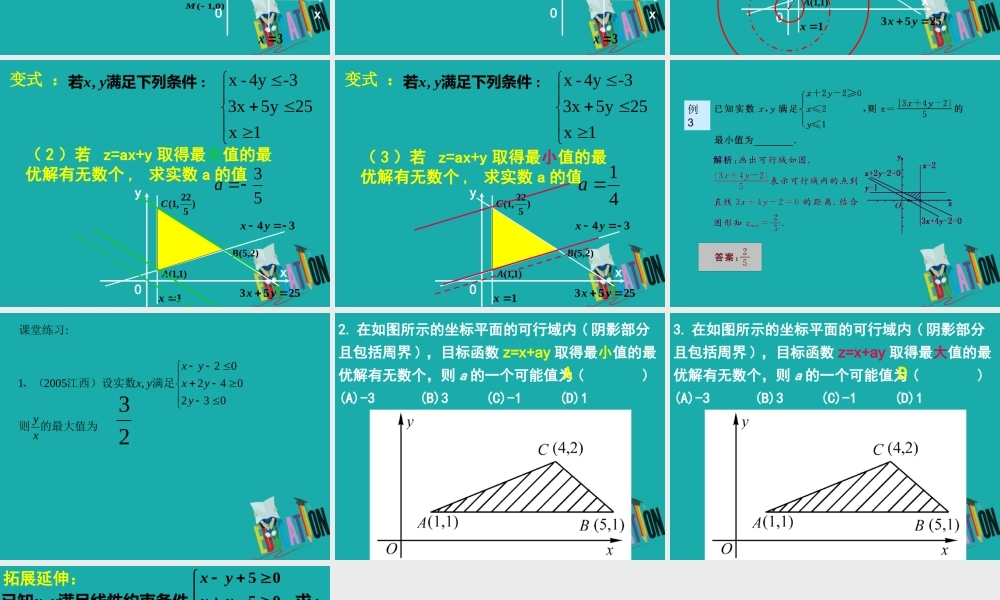
551ABCOxy勤能补拙如果 C≠0, 可取 (0,0);如果 C ＝ 0, 可取 (1,0) 或 (0,1). 二元一次不等式 Ax+By+C>0 在平面直角坐标系中表示直线 Ax+By+C=0 某一侧所有点组成的平面区域。 确定步骤： (1) 直线定界 注意“>0 ( 或 <0) ” 时 , 直线画成虚线 ;“≥0( 或≤ 0)” 时 , 直线画成实线 .(2) 特殊点定域 注意 :小诀窍 看 y 的系数 B 和不等号的方向解线性规划题目的一般步骤：1 、画：画出线性约束条件所表示的可行域；2 、移：在线性目标函数所表示的一组平行线中，利用平移找出与可行域有公共点且纵截距最大或最小的直线；3 、求：通过解方程组求出最优解；4 、答：做出答案。:30505,求满足线性约束条件已知xyxyxyx的最值xyZ xy03x05  yx05  yx)5,0(A)2,3(B)8,3(C32为最大值不存在，最小值),(yxP例 1 ：:30505,求满足线性约束条件已知xyxyxyx的最值1xyZxy03x05  yx05  yx)5,0(A)2,3(B)8,3(C215，最小值为最大值为),(yxP)0,1(M变式：:30505,求满足线性约束条件已知xyxyxyx的最值22yxZxy03x05  yx05  yx)5,0(A)2,3(B)8,3(C22573，最小值为最大值为),(yxP例 2 ：的最值求22)1(yxZ:, 满足下列条件若yx1x 25 5y3x-34y -x变式：xy01x34yx2553yx)1,1(A)2,5(B)522,1(CPZmax=29 Zmin=2（ 2 ）若 z=ax+y 取得最大值的最优解有无数个 , 求实数 a 的值:, 满足下列条件若yx1x 25 5y3x-34y -x变式 ：xy01x34yx2553yx)1,1(A)2,5(B)522,1(C53a（ 3 ）若 z=ax+y 取得最小值的最优解有无数个 , 求实数 a 的值:, 满足下列条件若yx1x 25 5y3x-34y -x变式 ：xy01x34yx2553yx)1,1(A)2,5(B)522,1(C41a例3的最大值为则满足江西）设实数、（课堂练习xyyyxyxyx03204202,20051:232. 在如图所示的坐标平面的可行域内 ( 阴影部分且包括周界 ) ，目标函数 z=x+ay 取得最小值的最优解有无数个，则 a 的一个可能值为 ( ) (A)-3 (B)3 (C)-1 (D)1A3. 在如图所示的坐标平面的可行域内 ( 阴影部分且包括周界 ) ，目标函数 z=x+ay 取得最大值的最优解有无数个，则 a 的一个可能值为 ( )(A)-3 (B)3 (C)-1 (D)1D:30505,求满足线性约束条件已知xyxyxyx的最值122xyxZxy03x05  yx05  yx)5,0(A)2,3(B)8,3(C257，最小值为最大值为),(yxP)0,1(M拓展延伸：