数学 2.5从力做的功到向量的数量积(第1课时)教学课件 北师大版必修4 课件VIP免费

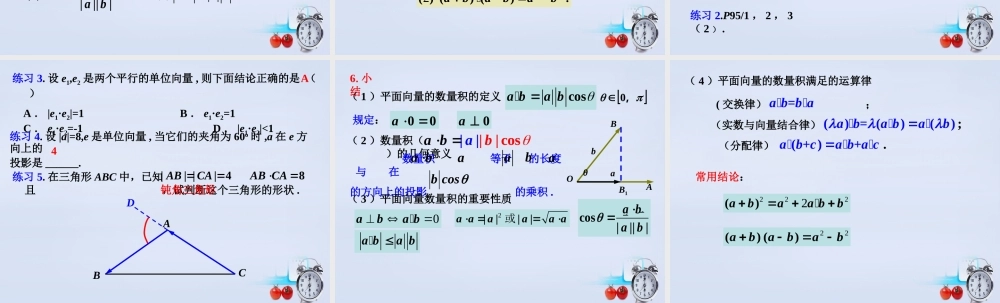
力的做功问题θsF 一个物体在力 F 的作用下产生的位移 s ，那么力 F 所做的功应当怎样计算？其中力 F 和位移 s 是向量， 是 F 与 s 的夹角，而功 W 是数量 .cosWF s1cosFFF2F1当 时， W>0, 即力 F 做正功；900当 时， W=0, 即力 F 的方向与位移 s的方向垂直，力 F 不做正功；90 当 时， W<0, 即力 F 做负功 .90180θsFOABab§5 从力做的功到向量的数量积（一）1. 两个非零向量的夹角ab记作：注意：共同的起点！ 两个非零向量 和 ，作 ， ，则 叫做向量 和 的夹角．AOB)1800(abOAa� OBb�ab若 ， 与 同向0abθab若 ， 与 反向180abOABba若 ， 与 垂直90abOABabOABba2. 平面向量的数量积的定义规定：零向量与任意向量的数量积为 0, 即.a  00注意 ! （ 1 ）两向量的数量积是一个数量，而不是向量，符号由夹角决定：当 时 , ；当 时 , ；当 时 , 090 __ 0a b90 __ 0a b90180__ 0.a b练习 1.P93/1 ， 2.a b记作 ，即 a ba bcos（ 3 ） 不能写成 或 ．a babab例 1. 已知 与 的夹角 ，求aba5,4,135a b.b（ 2 ）规定零向量可与任一向量垂直 . 已知两个非零向量 和 ，它们的夹角为 ，则数量 叫做 与 的数量积（或内积），aba bcosbaAabθBB1OBAθbB1aOθBb(B1)AaO如图：OAa OBb,.�b cos 叫做 在 方向上的投影 . ba3. 数量积（ ） 的几何意义a bba|||| cos  数量积 等于 的长度 与 在 的方向上的投影 的乘积 .bbaaaacosb注意！bRcos.在 方向上的投影ba4. 平面向量数量积的重要性质特别地2 ||||.a aaaa a或4( ) cos.||||a ba ba bab|||| cos 设 、 都是非零向量， 是与 方向相同的单位向量， 是与 的夹角 .a bebae(1)cos ;e aa ea(2)0;aba ba ba b（ 3 ）当 与 同向时， ； 当 与 反向时， . abab...