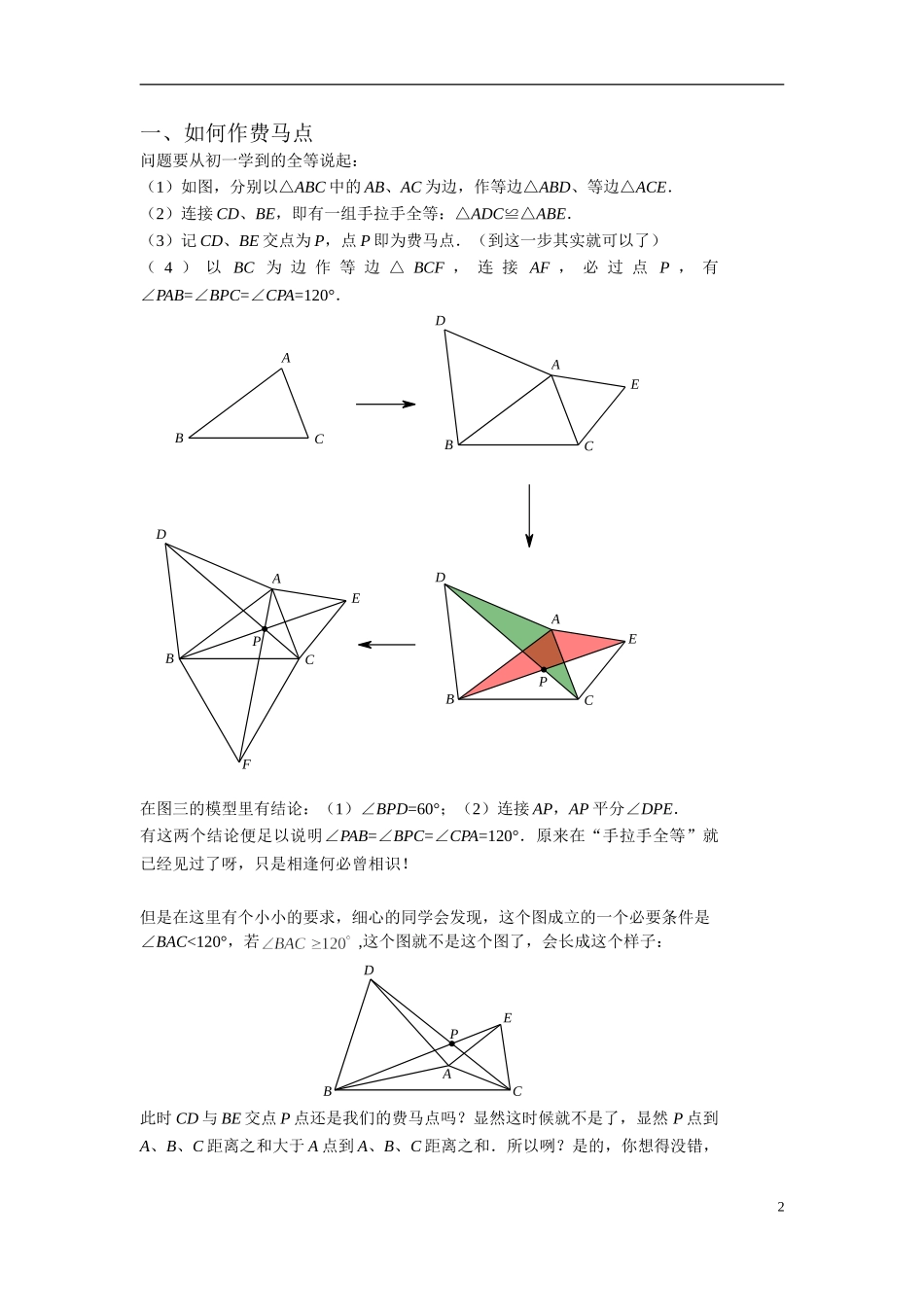
最值系列之费马点皮耶·德·费马,17 世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.据说费马在提出“费马大定理”时,在笔记本上写道:我已经想到了一个绝妙的证明方法但是这个地方不够写,我就不写了吧。看得出那个时候纸确实挺贵的,然后,直到 1995 年,才由英国数学家怀尔斯证明出,而距离费马逝世,已经过去了 330 年.果然,数学搞得好的都是装 x 的一把好手.言归正传,今天的问题不是费马提出来的,是他解决的,故而叫费马点.问题:在△ABC 内找一点 P,使得 PA+PB+PC 最小.ABCP【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.阿哈哈哈,此处一个也用不上!其实理论还是上面的理论,本题难点在于有 3 条线段,我们需要对这三条线段作一些位置上的变化,如果能变换成在一条直线上,问题就能解决了!算了算了,不墨迹了,直接报答案了:若点 P 满足∠PAB=∠BPC=∠CPA=120°,则 PA+PB+PC 值最小,P 点称为该三角形的费马点.接下来讨论 3 个问题:(1)如何作三角形的费马点?(2)为什么是这个点?(3)费马点怎么考?1一、如何作费马点问题要从初一学到的全等说起:(1)如图,分别以△ABC 中的 AB、AC 为边,作等边△ABD、等边△ACE.(2)连接 CD、BE,即有一组手拉手全等:△ADC≌△ABE.(3)记 CD、BE 交点为 P,点 P 即为费马点.(到这一步其实就可以了)( 4 ) 以 BC 为 边 作 等 边 △ BCF , 连 接 AF , 必 过 点 P , 有∠PAB=∠BPC=∠CPA=120°.FPPABCDEEDCBABACABCDE在图三的模型里有结论:(1)∠BPD=60°;(2)连接 AP,AP 平分∠DPE.有这两个结论便足以说明∠PAB=∠BPC=∠CPA=120°.原来在“手拉手全等”就已经见过了呀,只是相逢何必曾相识!但是在这里有个小小的要求,细心的同学会发现,这个图成立的一个必要条件是∠BAC<120°,若 ,这个图就不是这个图了,会长成这个样子:ABCDEP此时 CD 与 BE 交点 P 点还是我们的费马点吗?显然这时候就不是了,显然 P 点到A、B、C 距离之和大于 A 点到 A、B、C 距离之和.所以咧?是的,你想得没错,2此时...