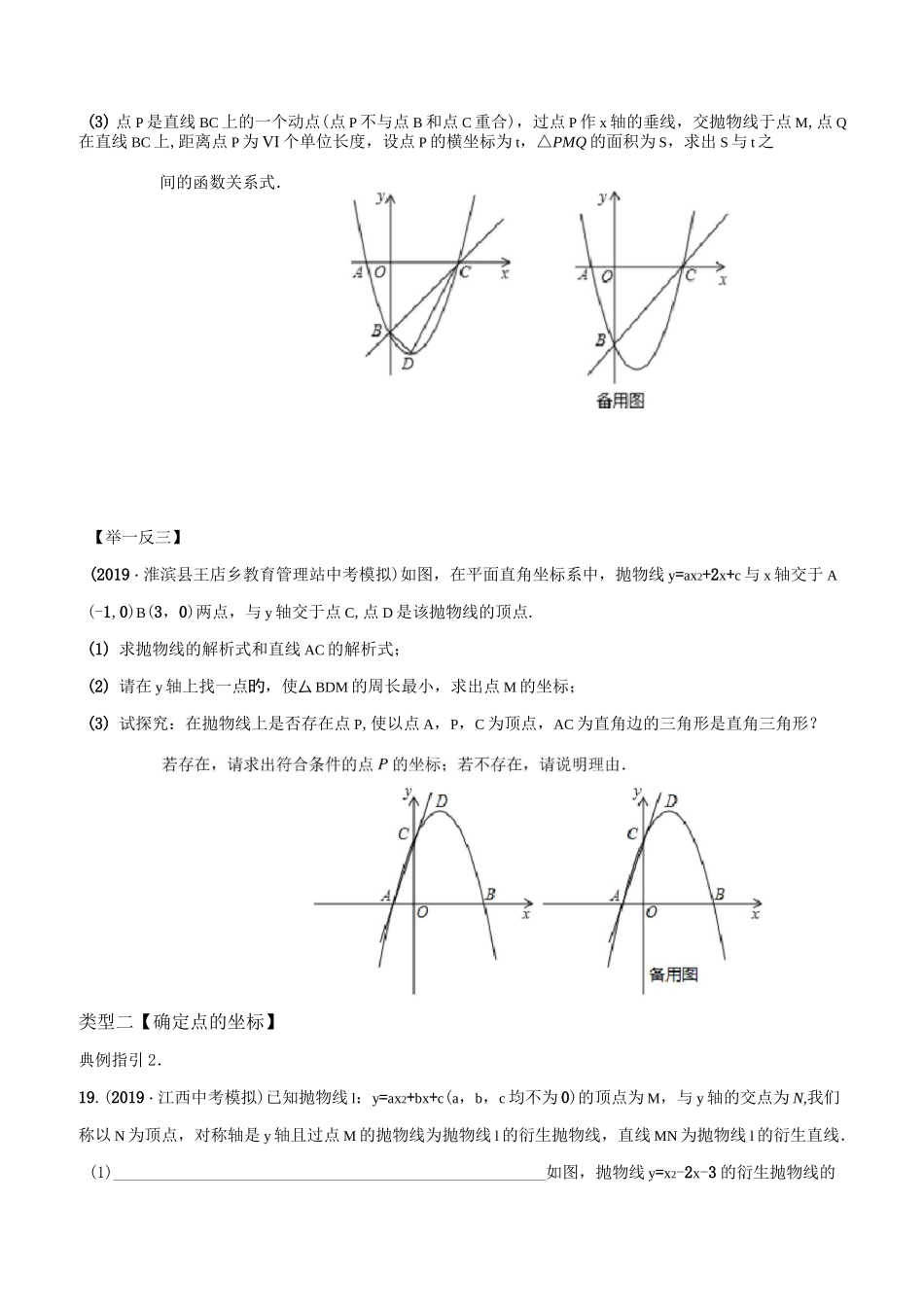
专题一直角三角形的存在性问题【考题研究】这类问题主要是已知直角三角形的一边(即直角三角形的两个点确定),求解第三点。这类问题主要是和动点问题结合在一起,主要在于考查学生的探寻能力和分类研究的推理能力,也是近几年来各市地对学生能力提高方面的一个考查。【解题攻略】解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.在平面直角坐标系中,两点间的距离公式常常用到.怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点).【解题类型及其思路】当直角三角形存在时可从三个角度进行分析研究:(1)当动点在直线上运动时,常用的方法是①k-k=-1,② 三角形相似,③勾股定理;(2)当动点在曲线上运动时,情况分类如下,第一当已知点处12作直角的方法① k-k=-1,② 三角形相似,③勾股定理;第二是当动点处作直角的方法:寻找特殊角12【典例指引】类型一【确定三角形的形状】典例指引 1.(2019・辽宁中考模拟)已知,m,n 是一元二次方程 x2+4x+3=0 的两个实数根,且 ImlVlnl,抛物线y=x2+bx+c 的图象经过点 A(m,0),B(0,n),如图所示.(1)求这个抛物线的解析式;(2)设(1)中的抛物线与 x 轴的另一个交点为抛物线的顶点为 D,求出点 C,D 的坐标,并判断厶 BCD 的形状;(3) 点 P 是直线 BC 上的一个动点(点 P 不与点 B 和点 C 重合),过点 P 作 x 轴的垂线,交抛物线于点 M,点 Q在直线 BC 上,距离点 P 为 VI 个单位长度,设点 P 的横坐标为 t,△PMQ 的面积为 S,求出 S 与 t 之间的函数关系式.【举一反三】(2019・淮滨县王店乡教育管理站中考模拟)如图,在平面直角坐标系中,抛物线 y=ax2+2x+c 与 x 轴交于 A(-1,0)B(3,0)两点,与 y 轴交于点 C,点 D 是该抛物线的顶点.(1) 求抛物线的解析式和直线 AC 的解析式;(2) 请在 y 轴上找一点旳,使厶 BDM ...