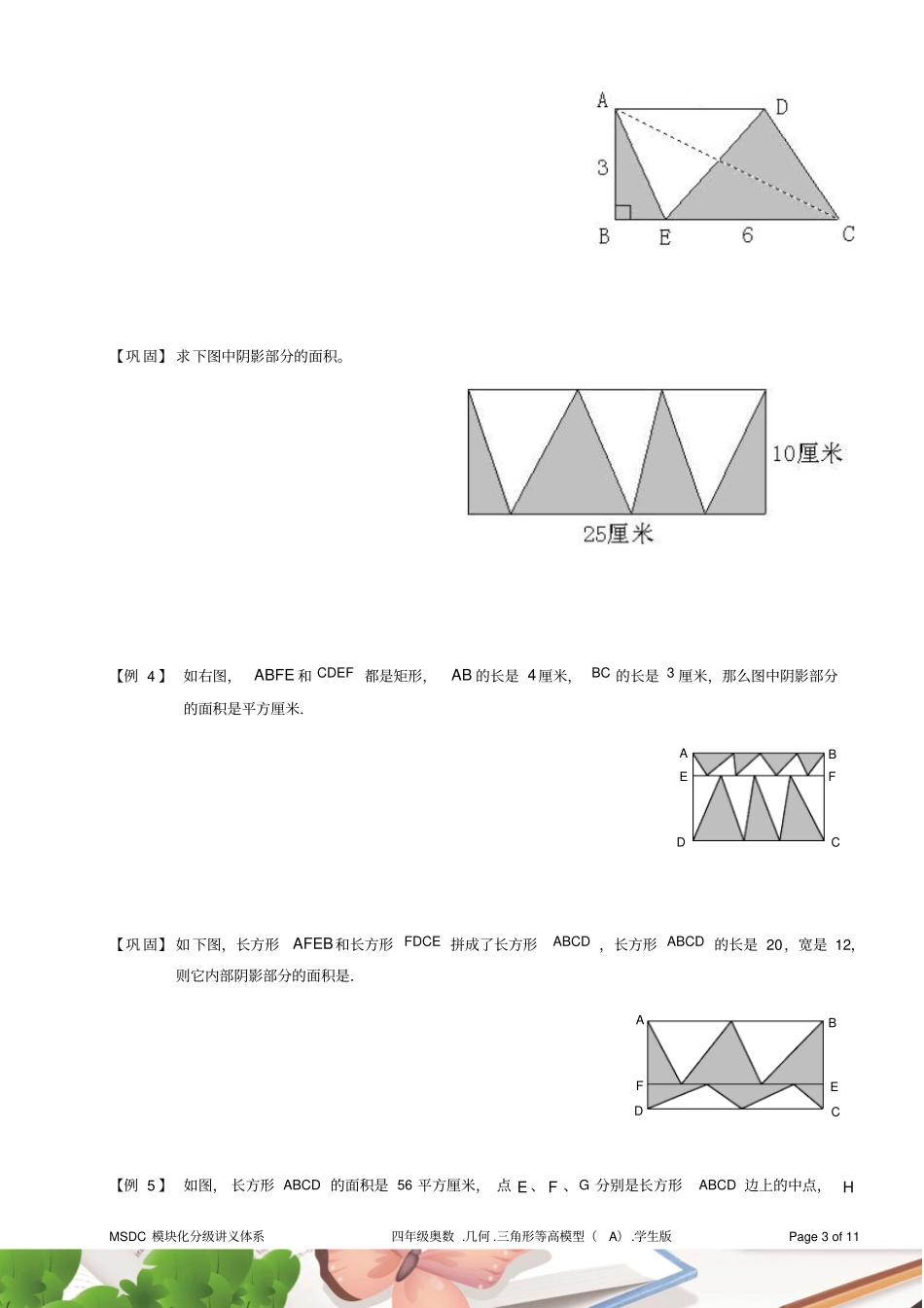
MSDC 模块化分级讲义体系四年级奥数 .几何 .三角形等高模型(A) .学生版Page 1 of 11三角形等高模型我们已经知道三角形面积的计算公式:三角形面积底高2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大( 小),三角形面积也就越大( 小 ) ;如果三角形的高不变,底越大( 小),三角形面积也就越大( 小 ) ;这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3 倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论:①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如左图12::SSa bbaS2S1DCBA③夹在一组平行线之间的等积变形,如右上图ACDBCDSS△△;反之,如果ACDBCDSS△△,则可知直线AB 平行于 CD .④等底等高的两个平行四边形面积相等( 长方形和正方形可以看作特殊的平行四边形) ;⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.知识框架等高三角形模型MSDC 模块化分级讲义体系四年级奥数 .几何 .三角形等高模型(A) .学生版Page 2 of 11【例 1 】 你有多少种方法将任意一个三角形分成 3 个面积相等的三角形.【巩 固】 你有多少种方法将任意一个三角形分成4 个面积相等的三角形.【例 2 】 如图, BD长 12 厘米, DC长 4 厘米, B、 C和 D在同一条直线上.⑴求三角形ABC的面积是三角形ABD面积的多少倍?⑵求三角形ABD的面积是三角形ADC面积的多少倍?DCBA【巩 固】 如右图, E 在 AD上, AD垂直 BC, AD=12 厘米, DE=3厘米。求:三角形EBC的面积是三角形ABC面积的几分之几?【例 3 】 如图, ABCD是直角梯形,求阴影部分的面积和。(单位:厘米)例题精讲MSDC 模块化分级讲义体系四年级奥数 .几何 .三角形等高模型(A) .学生版Page 3 of 11【巩 固】 求下图中阴影部分的面积。【例 4 】 如右图,ABFE ...