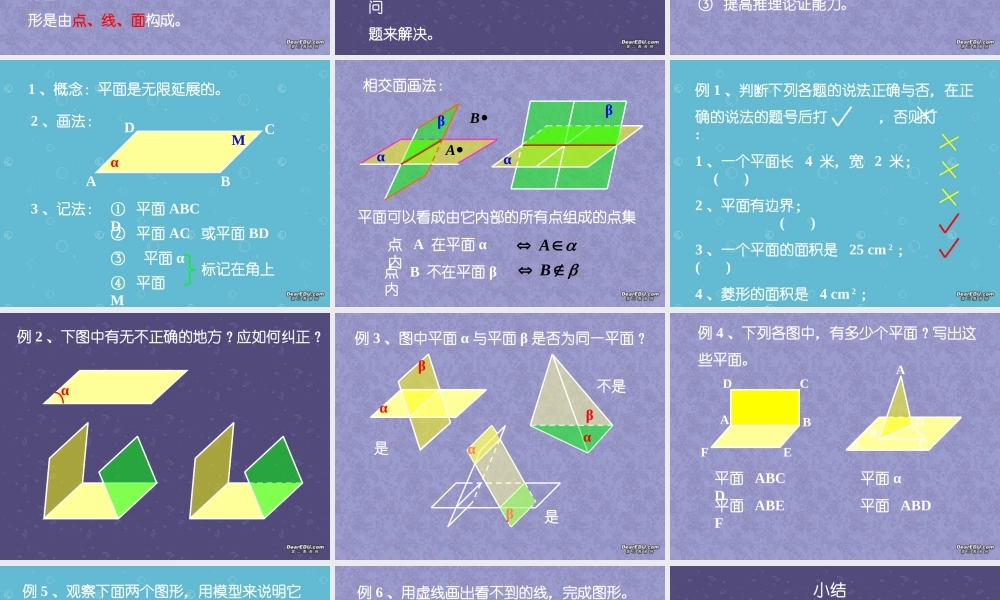
问题一:你能过任意一点引三条互相垂直的直线吗?墙角问题二:你能用六根火柴棍,在桌面上搭四个三角形吗?问题三:你能画出一个四边形,使它的对角线所在的直线不相交吗?折纸上述图形即为立体图形1 、平面图形与立体图形的联系与区别:联系:从集合论的角度看,两者都是点的 集合;区别:① 平面图形的点都在一个平面内,而立体图形的点不全在一个平面内; ② 平面图形由点、线构成,而立体图形是由点、线、面构成。2 、空间图形平面图形立体图形3 、立体图形的研究方法:① 考虑问题时,要着眼于整个空间,而不是局限于某一个平面;② 立体图形的问题常常转化为平面图形问题来解决。研究内容:空间的直线、平面和简单几何体及它们的几何性质、位置关系的判定、画法、度量计算以及相关的应用。学习要点:① 搞清平面图形和立体图形的联系与区别;② 发展空间想像能力;③ 提高推理论证能力。1 、概念:平面是无限延展的。2 、画法:ABCD3 、记法: ① 平面 ABCD② 平面 AC 或平面 BD③ 平面 αα④ 平面M标记在角上M相交面画法:αβαβ平面可以看成由它内部的所有点组成的点集AB点 A 在平面 α内 A点 B 不在平面 β内 B例 1 、判断下列各题的说法正确与否,在正确的说法的题号后打 ,否则打 :1 、一个平面长 4 米,宽 2 米; ( )2 、平面有边界; ( )3 、一个平面的面积是 25 cm 2 ; ( )4 、菱形的面积是 4 cm 2 ; ( )5 、一个平面可以把空间分成两部分 . ( )α例 2 、下图中有无不正确的地方?应如何纠正?例 3 、图中平面 α 与平面 β 是否为同一平面?αβαβαβ是是不是例 4 、下列各图中,有多少个平面?写出这些平面。ABCDFEABCDα平面 ABCD平面 ABEF平面 α平面 ABD例 5 、观察下面两个图形,用模型来说明它们的位置有什么不同,并用字母来表示各平面。例 6 、用虚线画出看不到的线,完成图形。小结1 、空间图形平面图形立体图形2 、平面是无限延展的。3 、画法:平行四边形4 、记法: ① 平面 ABCD② 平面 AC 或平面 BD③ 平面 α ④ 平面M思考:1 、能不能说一个平面长 3 米,宽 2 米? 为什么 ?2 、怎么画一个平面?3 、已知点 P 在平面 α 外,则记作 ________不能平行四边形P课后思:1 、制作空间四边形的模型,观察它的特征。2 、画一正方体,观察它有几个表面?几个顶点?3 、什么是公理?什么是定理?两者有何区别?4 、预习平面的基本性质。