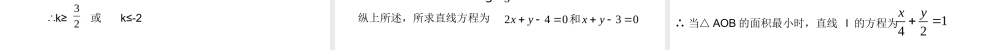7.2(4) 第七章直线和圆的方程全部课件 第七章直线和圆的方程全部课件VIP免费

2025年3月9日 一、知识要点：1. 以一个方程的解为坐标的点都是某条直线上的点；反过来，这条直线上点的坐标都是这个方程的解，这个方程叫做直线的方程，这条直线叫做方程的直线。2. 直线的倾斜角 α 的取值范围是________________0o ≤α ＜ 180o3. 经过两点 P1(x1,y1) 、 P2(x2,y2)(x1≠x2) 的直线的斜率公式是______________, 当 x1=x2 时，斜率 ________)(211212xxxxyyk不存在。4. 直线经过点 P1(x1,y1) 且斜率为 k 时，则其点斜式方程是____________, 当直线的倾斜角为 90o 时，直线没有点斜式方程，其方程可写成 _________.y-y1=k(x-x1)5. 直线的斜截式方程是 _________, 其中 ____ 表示直线在y 轴上的截距。x=x1y=kx+bb 6. 直线方程的两点式是 ____________ ，直线与坐标轴重合或与坐标轴 ____ 时，没有两点式方程，也就是两点式方程必须满足 _________________.121121xxxxyyyy平行y1≠y2 且 x1≠x21 byax7. 直线的截距式方程是 ________, 其中 应满足 ________ ，ba、,0,0ba8. 方程 Ax+By+C=0, （其中 A 、 B 不同时为 0 ）叫做直线方程的________.一般式。直线与坐标轴平行或重合或过原点时，没有截距式方程。 二、例题解析：例 1. 已知直线 x+ycotα+3=0(α 为锐角是常数），求直线的 倾斜角。解： α 是锐角，∴ cotα≠0 ，∴ 直线的斜率为tancot1)tan( 2∴ 直线的倾斜角为 π-α点评：求直线的倾斜角一般是先求直线的斜率，然后根据斜率写出直线的倾斜角。 例 2. 已知点 P(-1,1) 、 Q(2,2) ，直线 L ： y=kx-1 与线段 PQ相交，求实数 k 的范围。xyo12-1-112．Q(2,2)．P(-1,1)M(0,-1)L解 : 直线 L 的纵截距为 -1,∴ 直线过点 M(0,-1) L 与线段 PQ 相交 ,∴k ≥ kMQ 或 k≤kPM2302)1(2MQk201)1(1PMk∴k≥ 23或 k≤-2． 例 3. 直线 l 过点 (1,2) 和第一、二、四象限，若直线 l 的 横截距和纵截距之和为 6 ，求直线 l 的方程。 解：设直线 l 的横截距为 ， a6,a∴ 直线 l 的方程为16xyaa由题意可得纵截距为 点 (1,2) 在直线 l 上，121,6aa2560aa122,3aa解得21,4ya x当时，直线的方程为2直线经过一、二、四象限；31,3ya x当时，直线的方程为3直线经过一、二...