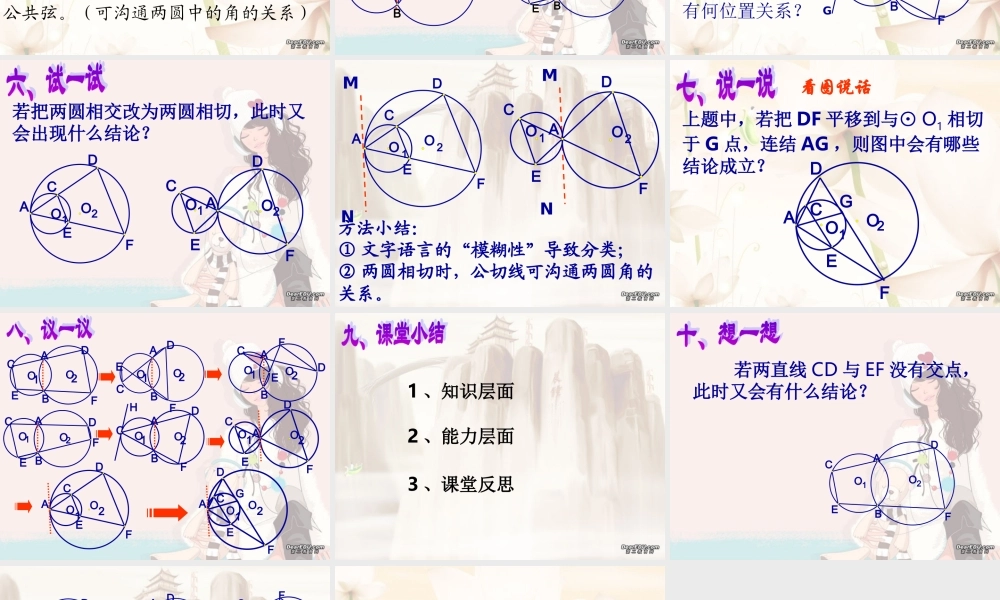
在探究中学习在学习中探究一道平面几何题的演变一道平面几何题的演变 已知:⊙ O1 和⊙ O2 相交于A 、 B 两点, O1 、 O2 位于 AB两侧,经过点 A 的直线 CD 与⊙ O1交于点 c ,与⊙ O2 交于点 D ,经过点 B 的直线 EF 与⊙ O1 交于点 E ,与⊙ O2 交于点 F ,连结 CE 、 DF ,试画出图形。FDBAO1O2CEFDBAO1O2CEFDBAO1O2CEFDBAO1O2CE图中 CE 与 DF 有何位置关系?你是怎样猜测的?FDBAO1O2CEFDBAO1O2CEFDBAO1O2CEFDBAO1O2CE你能证明你的猜想吗?方法小结:两圆相交常见辅助线——作公共弦。(可沟通两圆中的角的关系)FDBAO1O2CEFDBAO1O2CE你一定能行!!当直线 CD 、 EF 的交点在⊙ O2 内或⊙ O2 外时,结论是否成立?试证明你的结论。FDBAO1O2CEFDBAO1O2CE已知:如图⊙ O1 和⊙ O2 相交于 A 、B 两点, C 是⊙ O1 上一点,连结 CA 、CB 交⊙ O2 于点 D 、 F ,过点 C 作⊙ O1的切线 GH 。猜测 CH 与 DF有何位置关系?OHFDBAO12CG若把两圆相交改为两圆相切,此时又会出现什么结论?ECO2AO1DFCEO2AO1DF方法小结:① 文字语言的“模糊性”导致分类;② 两圆相切时,公切线可沟通两圆角的关系。MNMNECO 2AO 1DFCEO2AO1DF上题中,若把 DF 平移到与⊙ O1 相切于 G 点,连结 AG ,则图中会有哪些结论成立?看图说话FO2ECDAO1GFDBAO1O2CEFDBAO1O2CEFDBAO1O2CEFDBAO1O2CEOHFDBAO12CCEO2AO1DFECO2AO1DFECFDO2AO1G1 、知识层面2 、能力层面3 、课堂反思 若两直线 CD 与 EF 没有交点,此时又会有什么结论?FDBAO1O2CEFDBAO1O2CEFDBAO1O2CEFDBAO1O2CEFDBAO1O2CEOHFDBAO12CCEO2AO1DFECO2AO1DFECFDO2AO1G