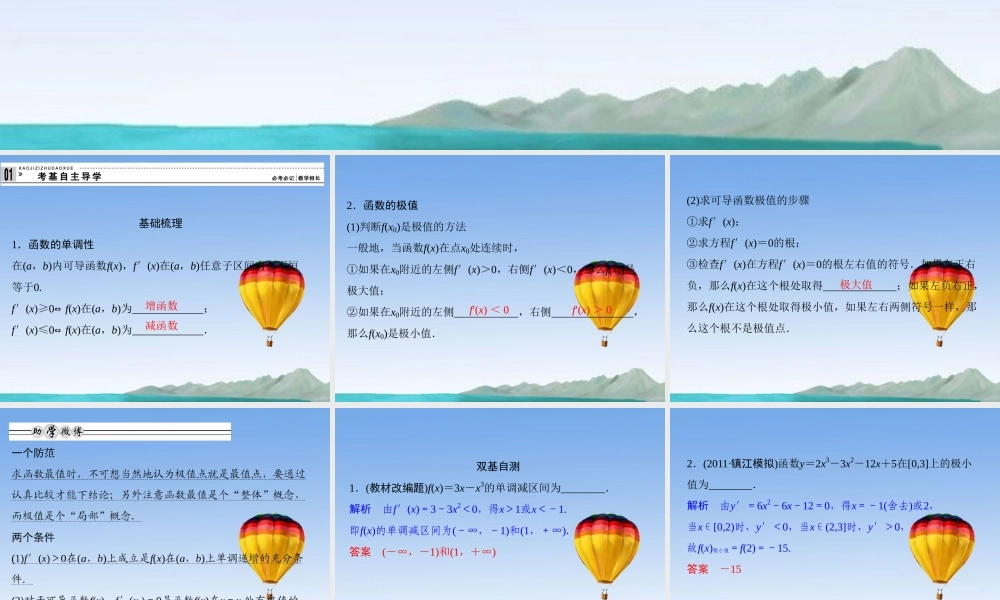
第 14 讲 用导数研究函数的单调性与极值 基础梳理 1.函数的单调性 在(a,b)内可导函数f(x),f′(x)在(a,b)任意子区间内都不恒等于0. f′(x)≥0⇔ f(x)在(a,b)为 ; f′(x)≤0⇔ f(x)在(a,b)为 . 增函数减函数2.函数的极值 (1)判断f(x0)是极值的方法 一般地,当函数f(x)在点x0处连续时, ①如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值; ②如果在x0附近的左侧 ,右侧 ,那么f(x0)是极小值. f′(x) < 0 f′(x) > 0(2)求可导函数极值的步骤 ①求f′(x); ②求方程f′(x)=0的根; ③检查f′(x)在方程f′(x)=0的根左右值的符号.如果左正右负,那么f(x)在这个根处取得 ;如果左负右正,那么f(x)在这个根处取得极小值,如果左右两侧符号一样,那么这个根不是极值点. 极大值 双基自测 1.(教材改编题)f(x)=3x-x3的单调减区间为________. 解析 由f′(x)=3-3x2<0,得x>1或x<-1. 即f(x)的单调减区间为(-∞,-1)和(1,+∞). 答案 (-∞,-1)和(1,+∞) 2.(2011·镇江模拟)函数y=2x3-3x2-12x+5在[0,3]上的极小值为________. 解析 由y′=6x2-6x-12=0,得x=-1(舍去)或2, 当x∈[0,2)时,y′<0,当x∈(2,3]时,y′>0, 故f(x)极小值=f(2)=-15. 答案 -15 3.函数y=3x2-6ln x的单调增区间为________,单调减区间为________. 解析 y′=6x-6x=6x2-6x. 定义域为(0,+∞), 由y′>0,得x>1,∴增区间为(1,+∞); 由y′<0,得0<x<1,∴减区间为(0,1). 答案 (1,+∞) (0,1) 4.若函数f(x)=ax3+3x2-x恰有3个单调区间,则实数a的取值范围是________. 解析 由题意f′(x)=3ax2+6x-1=0有两个不相等的实数根,故 62+4×3a>0a≠0⇒ a>-3且a≠0. 答案 (-3,0)∪(0,+∞) 5.已知a>0,函数f(x)=x3-ax在[1,+∞)上是单调递增函数,则a的取值范围是________. 解析 f′(x)=3x2-a,由f(x)在[1,+∞)上单调递增函数,得f′(x)≥0在区间[1,+∞)上恒成立,即3x2-a≥0,x∈[1,+∞)恒成立,故实数a≤3x2在[1,+∞)上的最小值,即a≤3. 答案 (-∞,3] 考向一 利用导数解决函数的单调性问题 【例1】►已知f(x)=ex-ax-1. (1)求f(x)的单调增区间; (2)若f(x)在定义域R内单调递增,求a的取值范围. [审题视点] (1)通过f′(x)≥0求单调递增区间;(2)转化为恒成 函数在指定区间上单调递...