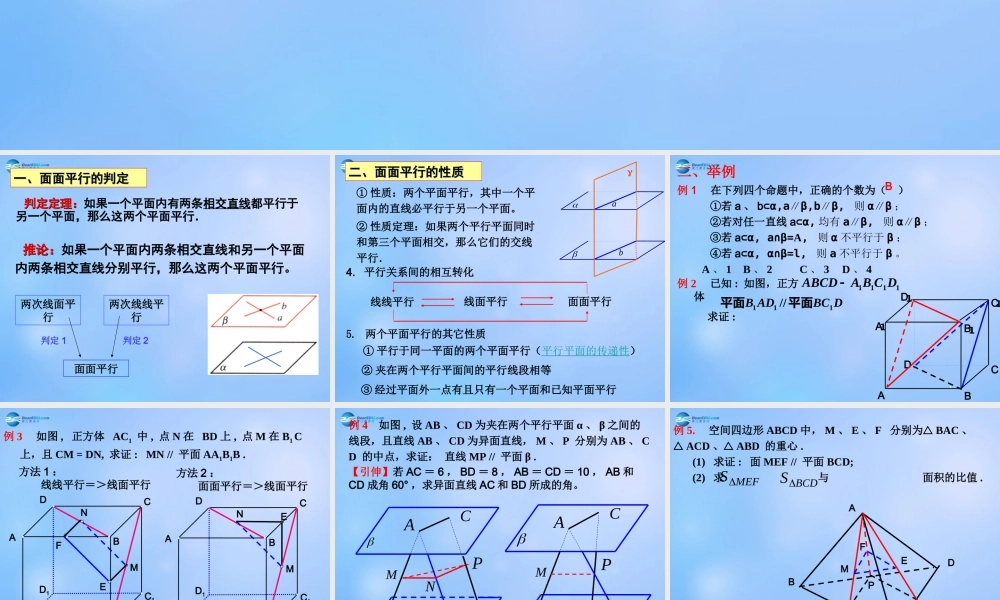
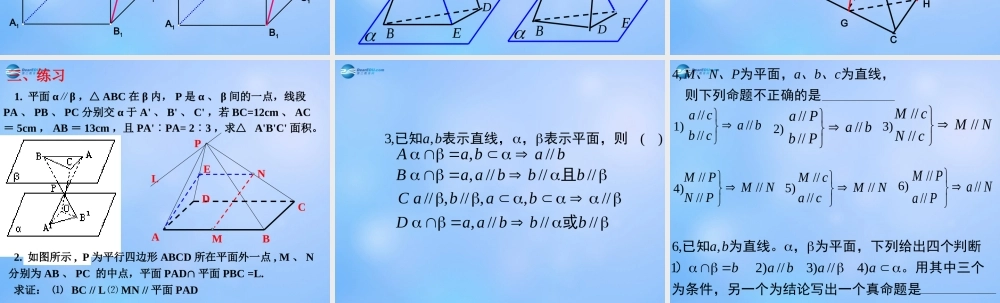
9.3 直线和平面平行与平面和平面平行2. 面面平行习题课 判定定理判定定理::如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.一、面面平行的判定一、面面平行的判定 推论:推论:如果一个平面内两条相交直线和另一个平面内两条相交直线分别平行,那么这两个平面平行。两次线线平行两次线面平行面面平行判定 1判定 2① 性质:两个平面平行,其中一个平面内的直线必平行于另一个平面。 ② 性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 4. 平行关系间的相互转化线线平行线面平行面面平行5. 两个平面平行的其它性质② 夹在两个平行平面间的平行线段相等③ 经过平面外一点有且只有一个平面和已知平面平行① 平行于同一平面的两个平面平行(平行平面的传递性)二、面面平行的性质二、面面平行的性质ba二、举例例 1 在下列四个命题中,正确的个数为( )①若 a 、 b⊂α,aβ,bβ, ∥∥则 αβ∥;②若对任一直线 a⊂α, 均有 aβ, ∥则 αβ∥;③若 a⊂α, a∩β=A, 则 α 不平行于 β ;④若 a⊂α, α∩β=l, 则 a 不平行于 β 。 A 、 1B 、 2 C 、 3D 、 4 B1DABDCBCA111例 2 已知 : 如图,正方体 求证 : 1111ABCDA B C D111//B ADBC D平面平面例 3 如图 , 正方体 AC1 中 , 点 N 在 BD 上 , 点 M 在 B1 C上,且 CM = DN, 求证 : MN // 平面 AA1B1B .D1A1BDCB1C1ANMFED1A1BDCB1C1ANME方法 1 : 线线平行=>线面平行方法 2 : 面面平行=>线面平行例 4 如图 , 设 AB 、 CD 为夹在两个平行平面 α 、 β 之间的线段,且直线 AB 、 CD 为异面直线, M 、 P 分别为 AB 、 CD 的中点,求证: 直线 MP // 平面 β .ADCBPMNEADCBPME【引伸】若 AC = 6 , BD = 8 , AB = CD = 10 , AB 和CD 成角 60° ,求异面直线 AC 和 BD 所成的角。例 5. 空间四边形 ABCD 中, M 、 E 、 F 分别为 BAC 、 ACD 、 ABD 的重心 . (1) 求证 : 面 MEF // 平面 BCD; (2) 求 与 面积的比值 .MEFSBCDSCAEDBGFMPH1. 平面 αβ∥ ,△ ABC 在 β 内, P 是 α 、 β 间的一点,线段 PA 、 PB 、 PC 分别交 α 于 A' 、 B' 、 C' ,若 BC=12cm 、 AC= 5cm , AB...