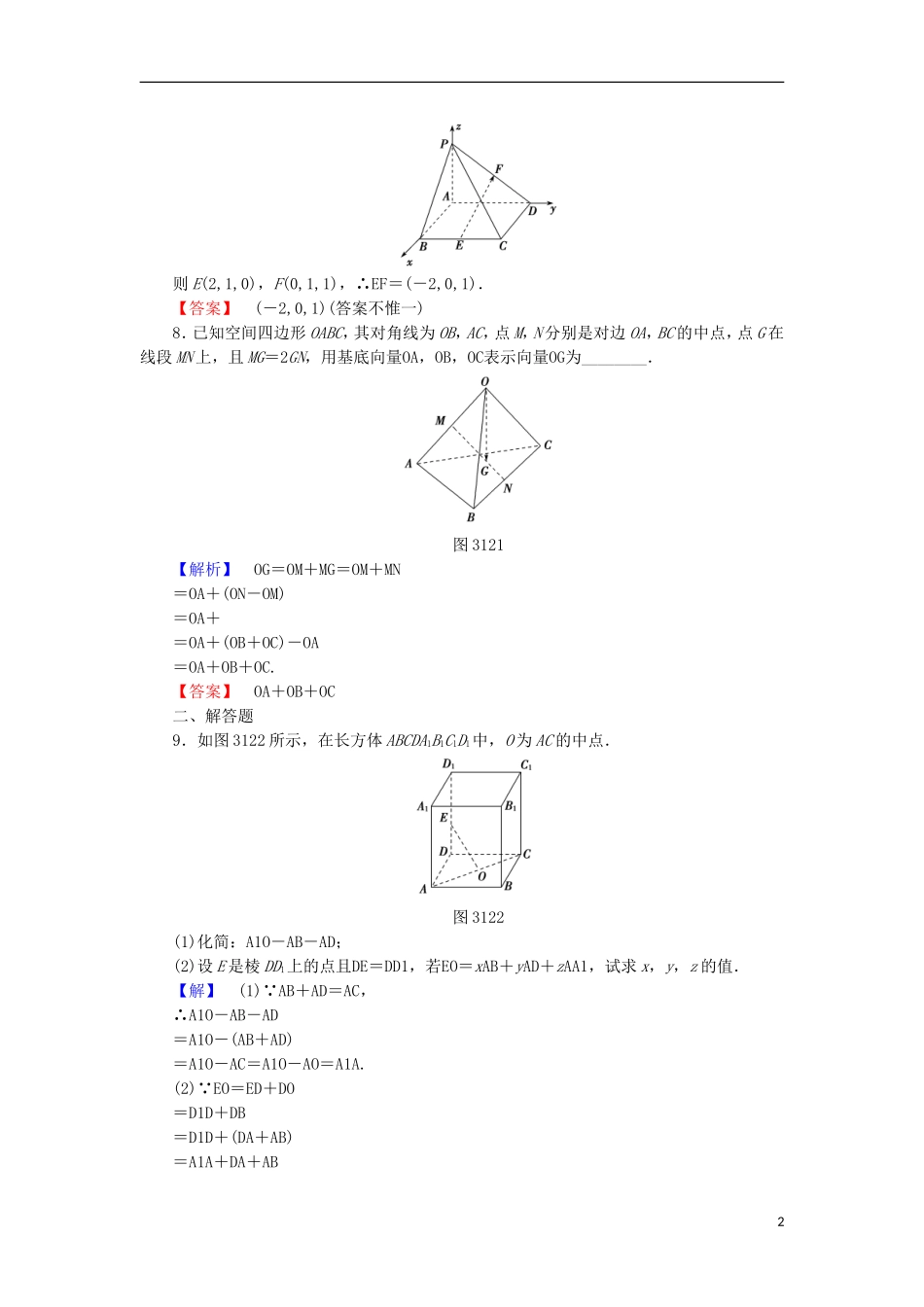
【课堂新坐标】2016-2017 学年高中数学 第 3 章 空间向量与立体几何 3.1.3 空间向量基本定理 3.1.4 空间向量的坐标表示学业分层测评 苏教版选修 2-1 (建议用时:45 分钟)学业达标]一、填空题1.若{a,b,c}是空间的一个基底,且存在实数 x,y,z 使得 xa+yb+zc=0,则 x,y,z 满足的条件是________.【解析】 由{a,b,c}是空间的一个基底知,a,b,c 不共面.由空间向量基本定理得 x=y=z=0.【答案】 x=y=z=02.已知 a=(1,-2,1),a-b=(-1,2,-1),则 b=________.【解析】 b=a-(a-b)=(1,-2,1)-(-1,2,-1)=(2,-4,2).【答案】 (2,-4,2)3.若 a=(a1,a2,a3),b=(b1,b2,b3),则==是 a∥b 的________条件.【解析】 设===k,易知 a∥b,即条件具有充分性.又若 b=0 时,b=(0,0,0),显然有a∥b,但条件==显然不成立,所以条件不具有必要性.【答案】 充分不必要4.若{a,b,c}是空间的一个基底,向量 m=a+b,n=a-b,则向量 a,b,c 中与 m,n 可以构成空间向量另一个基底的向量是________.【解析】 显然 a 或 b 均与 m,n 共面,c 与 m,n 不共面,故为 c.【答案】 c5.如图 3120 所示,设 O 为▱ABCD 所在平面外任意一点,E 为 OC 的中点,若AE=OD+xOB+yOA,则 x=_________,y=________.图 3120【解析】 AE=OE-OA=OC-OA=(OD+DC)-OA=OD+AB-OA=OD+(OB-OA)-OA=OD+OB-OA,∴x=,y=-.【答案】 -6.已知 a=(2x,1,3),b=(1,-2y,9),若 a∥b,则 x=________,y=________.【解析】 a=(2x,1,3),b=(1,-2y,9),又 a∥b,显然 y≠0,∴==,∴x=,y=-.【答案】 -7.底面为正方形的四棱锥 PABCD 中,PA⊥平面 ABCD,点 E,F 分别是 BC 和 PD 的中点,若PA=AB=2,则向量EF的坐标为________.【解析】 建立空间直角坐标系,如图所示.1则 E(2,1,0),F(0,1,1),∴EF=(-2,0,1).【答案】 (-2,0,1)(答案不惟一)8.已知空间四边形 OABC,其对角线为 OB,AC,点 M,N 分别是对边 OA,BC 的中点,点 G 在线段 MN 上,且 MG=2GN,用基底向量OA,OB,OC表示向量OG为________.图 3121【解析】 OG=OM+MG=OM+MN=OA+(ON-OM)=OA+=OA+(OB+OC)-OA=OA+OB+OC.【答案】 OA+OB+OC二、解答题9.如图 3122 所示,在长方体 ABCDA1B1C1D1中,O 为 AC 的中...