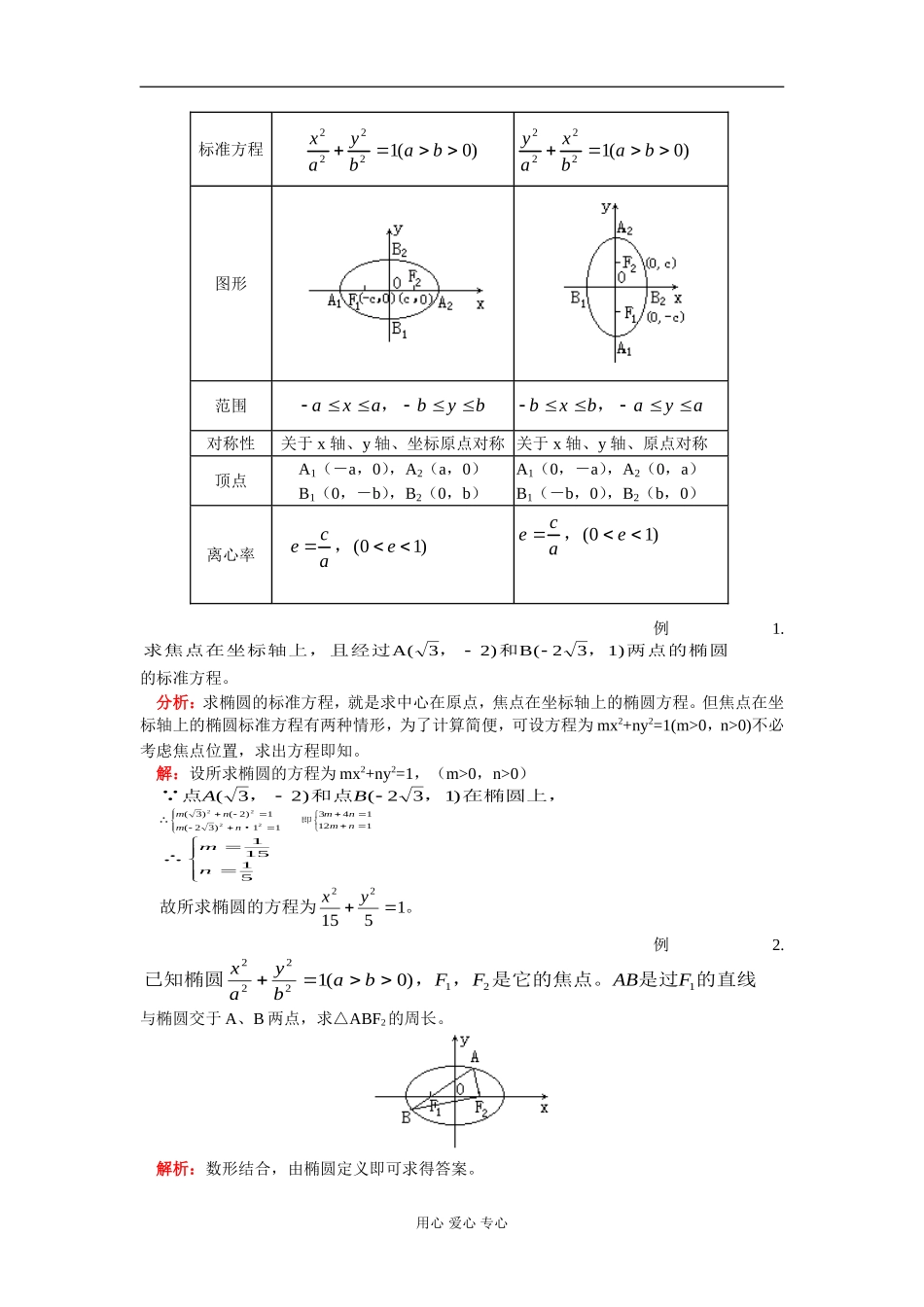
高二数学 椭圆 知识精讲 人教版一. 本周教学内容: 椭圆 教学目标: 1. 掌握椭圆的定义。(第一定义和第二定义)。 2. 能根据条件熟练求出椭圆的标准方程; 3. 掌握椭圆的几何性质及标准方程中的 a、b、c、e 的几何意义,及 a、b、c、e 间的相互关系; 4. 能综合应用椭圆的有关知识解决最值问题及参数的取值范围; 5. 理解直线与椭圆的位置关系,会求椭圆截直线所得的弦长,会应用弦中点的性质求解问题。 能力训练:进一步巩固求曲线方程的方法,提高运用坐标法的自觉性及解决几何问题的能力;进一步培养数形结合的能力;同时提高代数运算能力、综合分析问题解决问题的能力。二. 重点、难点: 重点:椭圆的定义、标准方程及几何性质的应用。 难点:椭圆的定义、标准方程、几何性质在解题过程中的灵活运用。【典型例题】一. 知识提要: 1. 椭圆的第一定义:平面内,与两个定点 F1、F2的距离和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。 2. 椭圆的第二定义: 平面内,动点与定点 ( , )的距离和它到定直线 :的距离的MFc0lxac2比是常数的点的轨迹是椭圆。定点是椭圆的焦点,定直线叫做椭ca acM() 0圆的准线,常数叫椭圆的离心率。ca 3. 椭圆的标准方程及几何性质:用心 爱心 专心标准方程 xaybab222210() yaxbab222210() 图形 范围 axabyb, bxbaya, 对称性 关于 x 轴、y 轴、坐标原点对称 关于 x 轴、y 轴、原点对称 顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0) 离心率 ecae,()01 ecae,()01 例1. 求焦点在坐标轴上,且经过,和,两点的椭圆A(32)B( 231)的标准方程。 分析:求椭圆的标准方程,就是求中心在原点,焦点在坐标轴上的椭圆方程。但焦点在坐标轴上的椭圆标准方程有两种情形,为了计算简便,可设方程为 mx2+ny2=1(m>0,n>0)不必考虑焦点位置,求出方程即知。 解:设所求椭圆的方程为 mx2+ny2=1,(m>0,n>0) 点,和点,在椭圆上,AB()()32231 ∴·即mnmnmnmn()()()32123113411212222 ∴mn11515 故所求椭圆的方程为。xy221551 例2. 已知椭圆,,是它的焦点。是过的直线xaybabFFABF222212...