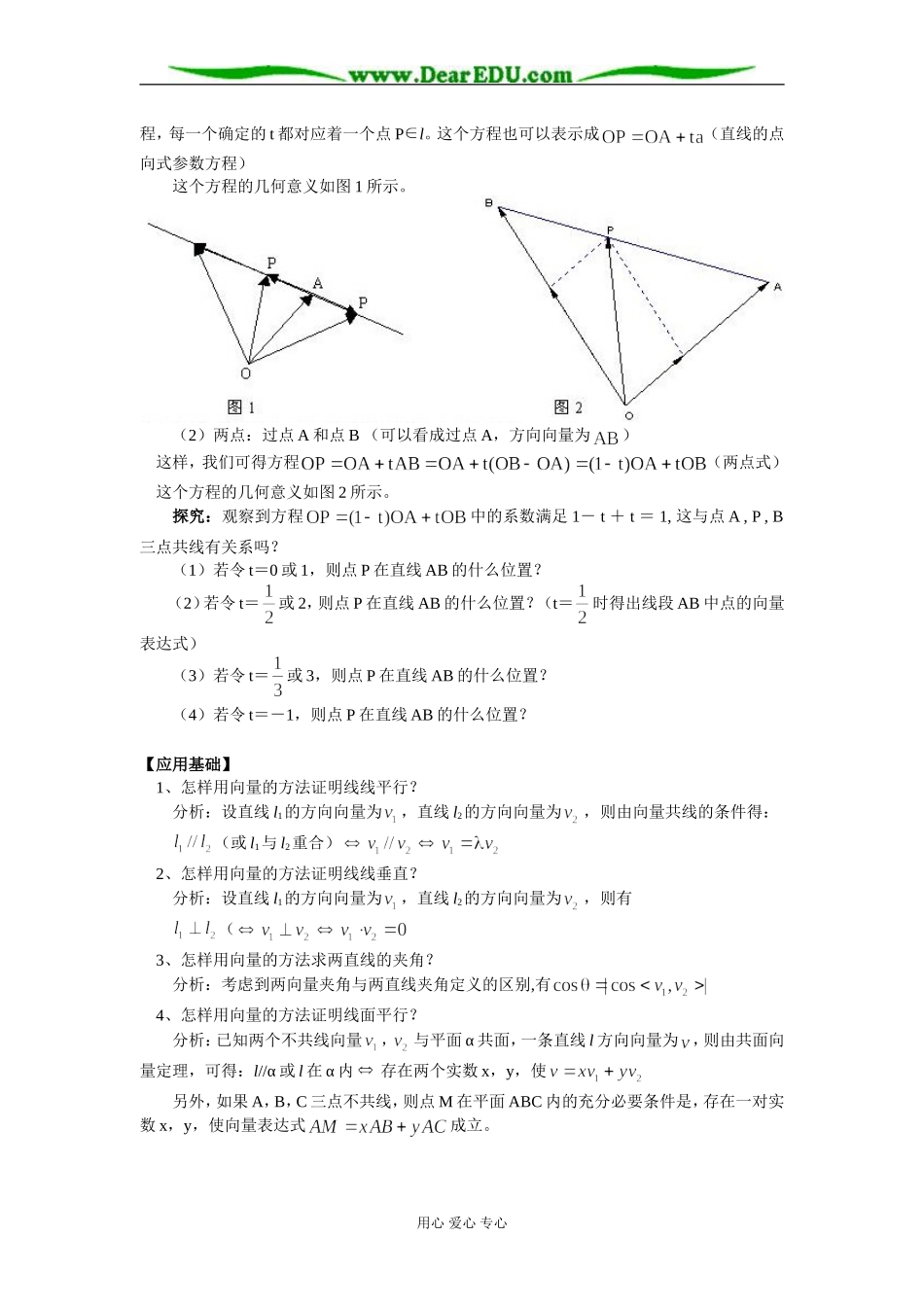
高二数学直线的方向向量与直线的向量方程知识精讲 人教实验版(B)【本讲教育信息】一. 教学内容:3.2.1 直线的方向向量与直线的向量方程3.2.2 平面的法向量与平面的向量表示二. 教学目的:1、掌握用向量表示直线的方法及确定点在直线上的位置的方法;会用向量的方法证明线线平行、线面平行、面面平行;能通过向量计算求证两条直线垂直或求两条直线所成的角。2、(1)理解平面的法向量的概念,并会求平面的法向量;(2)了解平面法向量的应用,并能用法向量论证相关的立体几何问题;(3)掌握正射影的概念,并能作出简单图形 F 在某一平面内的正射影 F0,并说出其图形的形状;(4)掌握三垂线定理及其逆定理,并能应用此定理解题。三. 教学重点、难点 重点:(1)直线的方向向量,平行关系的论证,用向量运算求证两条直线垂直或求两条直线所成的角。(2)平面法向量的概念及其应用,正射影的概念,三垂线定理及逆定理;难点:(1)直线的方向向量,平面 α 的共面向量的选取及其表示。 (2)对平面法向量的理解及灵活运用,三垂线定理的证明思路及三垂线定理的应用。四. 知识分析3.2.1 直线的方向向量与直线的向量方程1、思考:如何确定空间中的点的位置?分析:确定平面内点的位置,通常采用两个方法――“平面直角坐标系”或“该点相对于某一已知点的方向及距离”。那么,空间内呢?我们也可以用“该点的空间直角坐标系(x,y,z)”或“在空间中该点相对于某一已知点的方向及距离”来描述。注意:两个词――-“方向”、“距离”,给我们什么启示?结论:在空间我们可以用向量确定空间一点的位置或点的集合。【位置向量】 已知向量,在空间固定一个基点 O,再作向量,则点 A 在空间的位置就被向量所惟一确定了。这时,我们称这个向量为位置向量。注:“基点”是必需的;相对于确定的基点来说,空间内的点与向量有了一一对应关系。2、思考:如何确定空间中的直线?分析:在平面内确定直线通常采用的是“点向”和“两点”,那么空间中呢?探究:通过实际观察,在空间中我们仍旧可以采用“点向”或“两点”来确定直线。问题是如何操作呢?方案:求轨迹的一般步骤(1)点向:过点 A,且平行于向量 设 P 为直线上任一点,则有,故存在,使 ① ,这样直线上每一个点 P都与惟一的一个实数 t 相对应,向量方程就是过 A 且方向向量为的直线的参数方用心 爱心 专心程,每一个确定的 t 都对应着一个点 Pl。这个方程也...