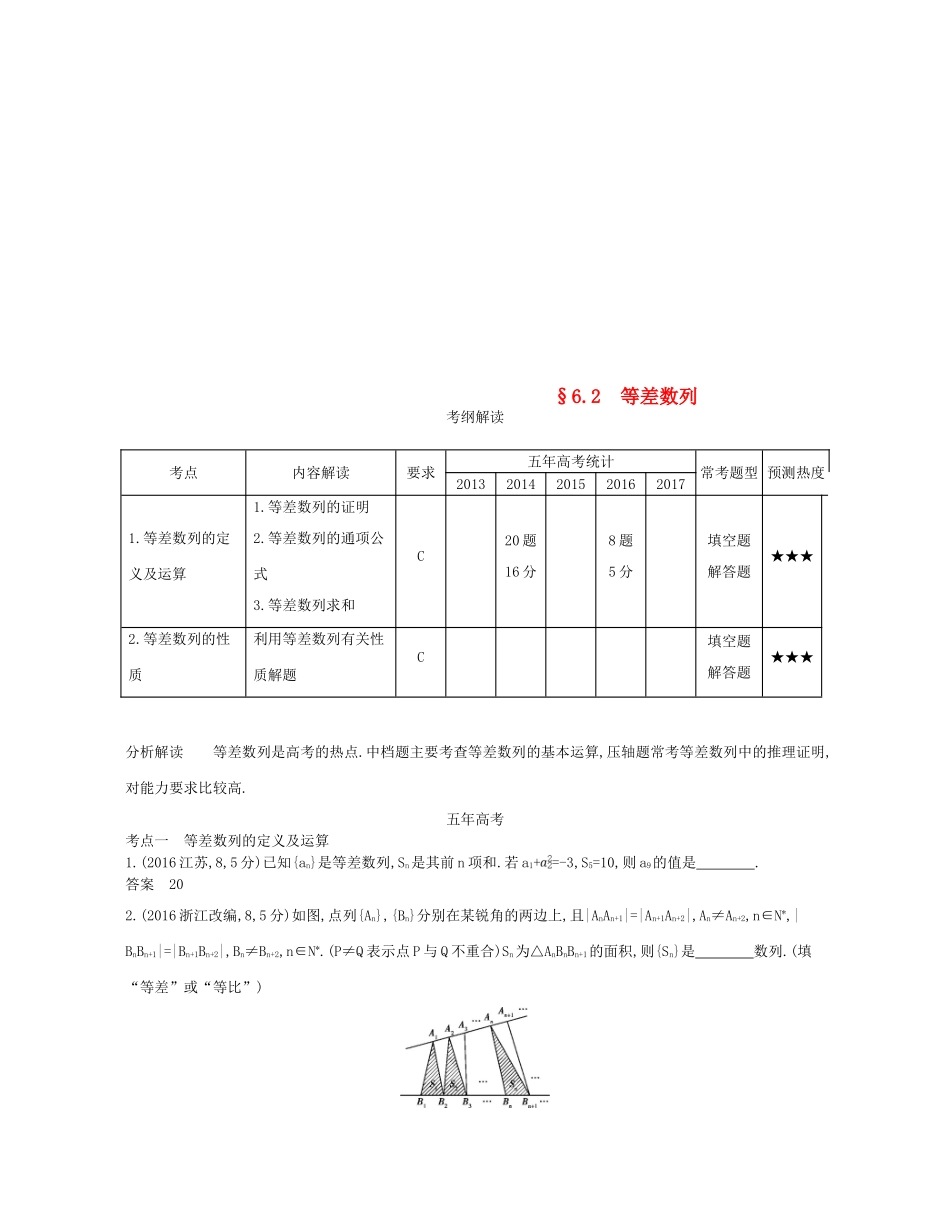
§6.2 等差数列考纲解读考点内容解读要求五年高考统计常考题型 预测热度201320142015201620171.等差数列的定义及运算1.等差数列的证明2.等差数列的通项公式3.等差数列求和C20 题16 分8 题5 分填空题解答题★★★2.等差数列的性质利用等差数列有关性质解题C 填空题解答题★★★分析解读 等差数列是高考的热点.中档题主要考查等差数列的基本运算,压轴题常考等差数列中的推理证明,对能力要求比较高.五年高考考点一 等差数列的定义及运算1.(2016 江苏,8,5 分)已知{an}是等差数列,Sn是其前 n 项和.若 a1+ =-3,S5=10,则 a9的值是 . 答案 202.(2016 浙江改编,8,5 分)如图,点列{An},{Bn}分别在某锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*.(P≠Q 表示点 P 与 Q 不重合)Sn为△AnBnBn+1的面积,则{Sn}是 数列.(填“等差”或“等比”) 答案 等差3.(2014 福建改编,3,5 分)等差数列{an}的前 n 项和为 Sn,若 a1=2,S3=12,则 a6等于 . 答案 124.(2013 课标全国Ⅰ理改编,7,5 分)设等差数列{an}的前 n 项和为 Sn,若 Sm-1=-2,Sm=0,Sm+1=3,则 m= . 答案 55.(2017 课标全国Ⅰ文,17,12 分)记 Sn为等比数列{an}的前 n 项和.已知 S2=2,S3=-6.(1)求{an}的通项公式;(2)求 Sn,并判断 Sn+1,Sn,Sn+2是否成等差数列.解析 (1)设{an}的公比为 q,由题设可得解得 q=-2,a1=-2.故{an}的通项公式为 an=(-2)n.(2)由(1)可得 Sn==- +(-1)n·.由于 Sn+2+Sn+1=- +(-1)n·=2=2Sn,故 Sn+1,Sn,Sn+2成等差数列.6.(2014 江苏,20,16 分)设数列{an}的前 n 项和为 Sn.若对任意的正整数 n,总存在正整数 m,使得 Sn=am,则称{an}是“H 数列”.(1)若数列{an}的前 n 项和 Sn=2n(n∈N*),证明:{an}是“H 数列”;(2)设{an}是等差数列,其首项 a1=1,公差 d<0.若{an}是“H 数列”,求 d 的值;(3)证明:对任意的等差数列{an},总存在两个“H 数列”{bn}和{cn},使得 an=bn+cn(n∈N*)成立.解析 (1)证明:由已知,得当 n≥1 时,an+1=Sn+1-Sn=2n+1-2n=2n.于是对任意的正整数 n,总存在正整数 m=n+1,使得Sn=2n=am.所以{an}是“H 数列”.(2)由已知,得 S2=2a1+d=2+d.因为{an}是“H 数列”,所以存在正整数 m,使得 S2=am,即 2+d=1+(m-1)d,于是(m-2)·d=1.因为 d<0,所以 m-2<0,故 m=1.从而 d=-1.当 d=-1 时,an=2-n,Sn=是小于 2 的整数,n∈N*.于是对任意的正整数 n,总存在正...