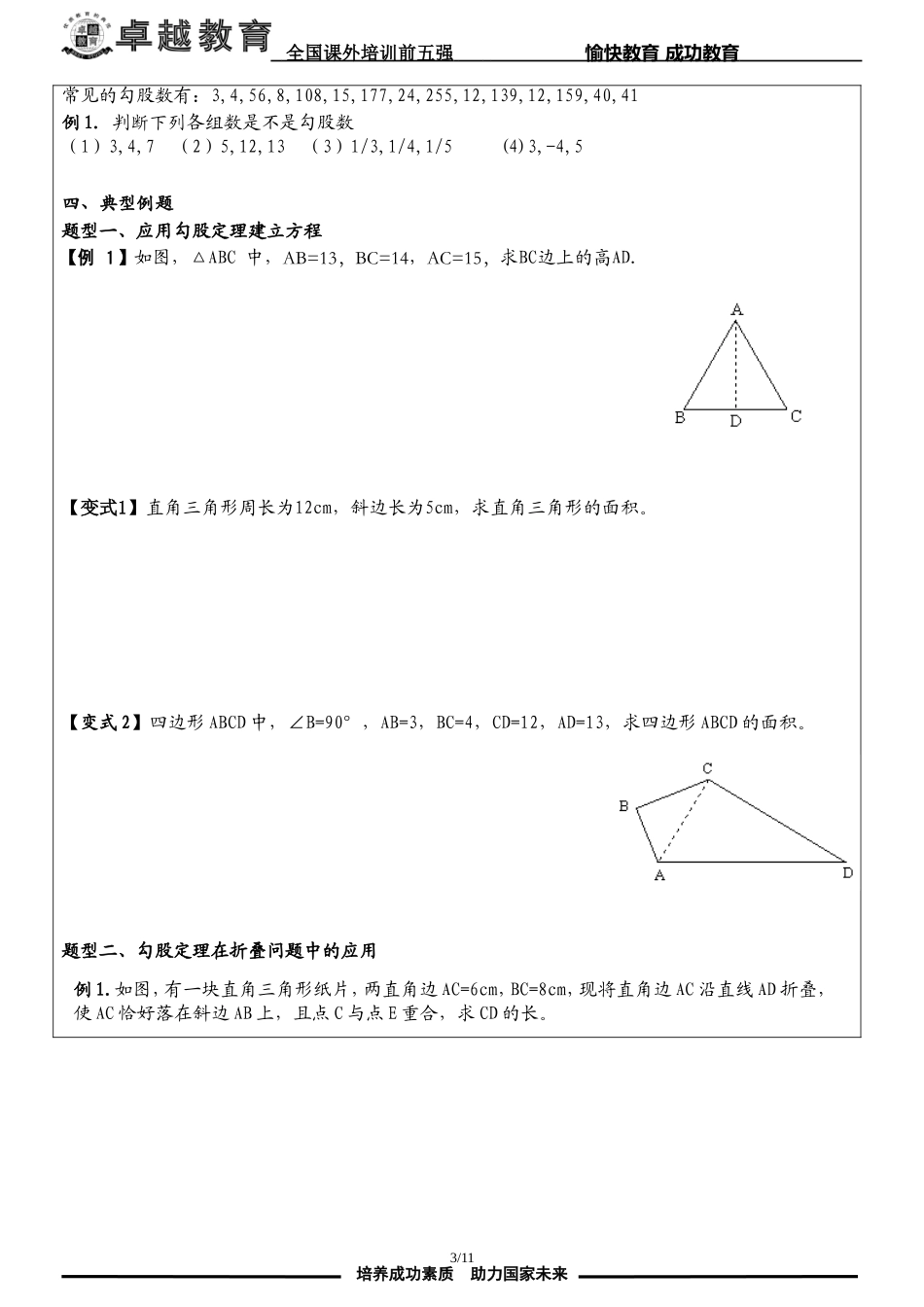
全国课外培训前五强愉快教育成功教育卓越教育教案专用学生姓名授课时间:授课科目:数学教学课题勾股定理知识点解析(二)重点、难点能准确证明勾股定理,并能将以灵活运用。教师姓名年级:初二课型:复习课一、作业检查作业完成情况:优□良□中□差□二、课前回顾对上次家庭作业进行检查并评讲三、知识整理知识点1.勾股定理(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方。如果用a,b和c分别表示直角三角形的两直角边和斜边(即:a2+b2=c2)注意:勾股定理揭示的是直角三角形三边关系的定理,只适用于直角三角形。应用勾股定理时,要注意确定那条边是直角三角形的最长边,也就是斜边,在Rt△ABC中,斜边未必一定是c,当∠A=90时,a2=b2+c2;当∠B=90时,b2=a2+c2例1.(1)如图1所示,在Rt△ABC中,∠C=90,AC=5,BC=12,求AB的长;(2)如图2所示,在Rt△ABC中,∠C=90,AB=25,AC=20,求BC的长(3)在Rt△ABC中,AC=3,BC=4,求AB2的值知识点2.勾股定理的证明(1)勾股定理的证明方法很多,可以用测量计算,可以用代数式的变形,可以用几何证明,也可以用面积(拼图)证明,其中拼图证明是最常见的一种方法。思路:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理1/11培养成功素质助力国家未来ACB图1CBA图2全国课外培训前五强愉快教育成功教育常见方法如下:方法一:,,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为大正方形面积为所以知识点3.直角三角形的判别条件(1)如果三角形的三边长啊a,b,c,满足a2+b2=c2足,那么这个三角形为直角三角形(此判别条件也称为勾股定理的逆定理)注意:在判别一个三角式是不是直角三角形时,a2+b2是否等于c2时需通过计算说明,不能直接写成a2+b2=c2。验证一个三角形是不是直角三角形的方法是:(较小边长)+(较长边长)=(最大边长)时,此三角形为直角三角形;否则,此三角形不是直角三角形.例1.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是()例2.在△ABC中,a=m2-n2,b=2mn,c=m2+n2,其中m,n是正整数,且m>n,试判断△ABC是不是直角三角形。知识点4.勾股数满足a2+b2=c2的三个正整数,称为勾股数。2/11培养成功素质助力国家未来cbaHGFEDCBAbacbaccabcabcbaHGFEDCBAbacbaccabcab全国课外培训前五强愉快教育成功教育常见的勾股数有:3,4,56,8,108,15,177,24,255,12,139,12,159,40,41例1.判断下列各组数是不是勾股数(1)3,4,7(2)5,12,13(3)1/3,1/4,1/5(4)3,-4,5四、典型例题题型一、应用勾股定理建立方程【例1】如图,△ABC中,AB=13,BC=14,AC=15,求BC边上的高AD.【变式1】直角三角形周长为12cm,斜边长为5cm,求直角三角形的面积。【变式2】四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积。题型二、勾股定理在折叠问题中的应用例1.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使AC恰好落在斜边AB上,且点C与点E重合,求CD的长。3/11培养成功素质助力国家未来全国课外培训前五强愉快教育成功教育【变式1】如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长。【变式2】在矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF.求DE的长;【变式3】如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上的一点.将矩形纸片沿着AE折叠,点B恰好落在边DC的点G处,求BE的长【变式4】在矩形纸片ABCD中,AB=3,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°,(1)BE的长为________,QF的长为_______;(2)四边形PEFH的面积为_______。4/11培养成功素质助力国家未来全国课外培训前五强愉快教育成功教育题型三、确定几何体上的最短路线例1、如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建子(图中虚线),并且要正好建到A点正上方的油罐顶...