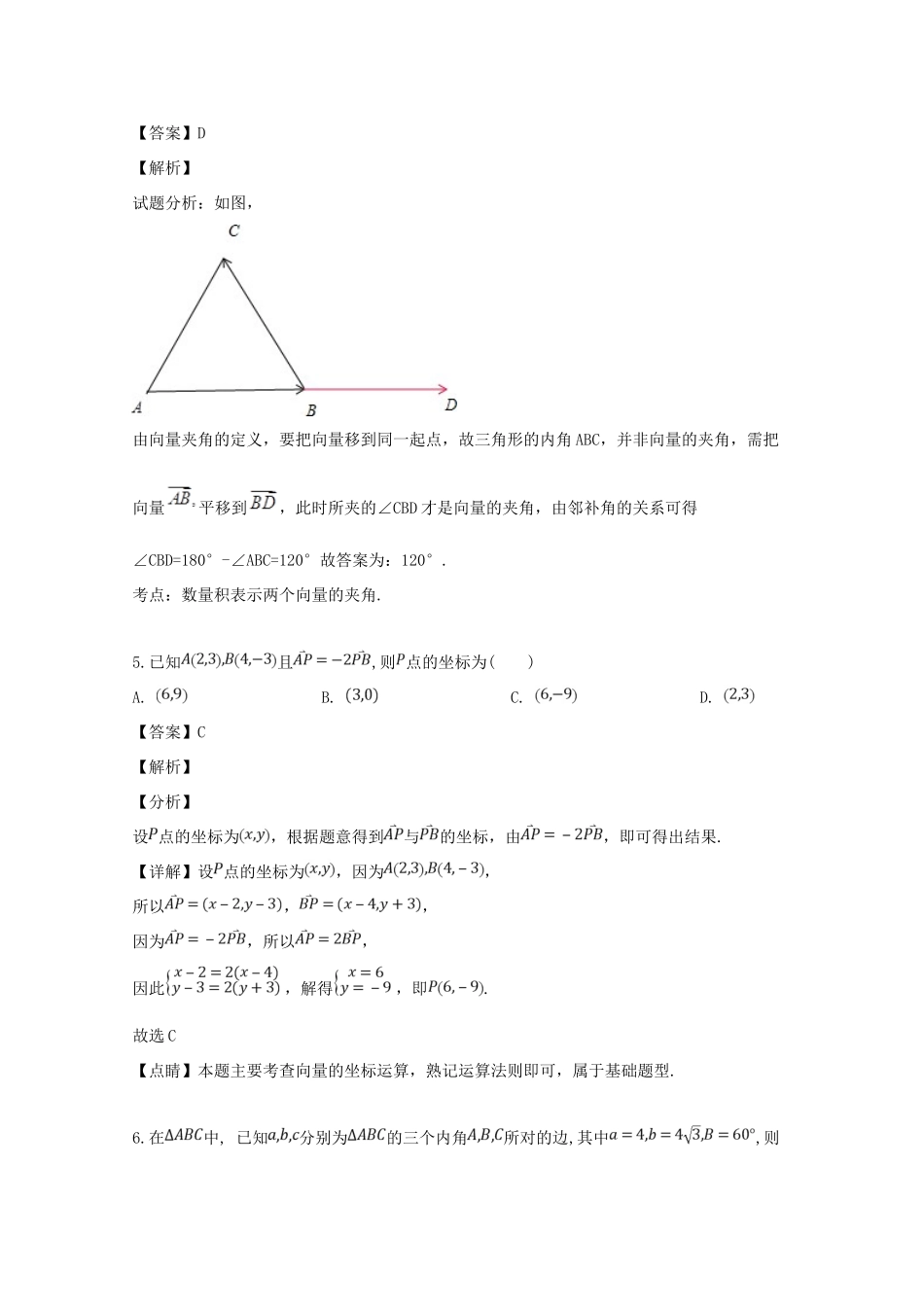
铜梁一中高 2021 届 2019 年春期高一(下)3 月考试数 学一、选择题(共 12 小题,每小题 5 分,共 60 分)1.已知为平行四边形,若向量,,则向量为( )A. B. C. D. 【答案】C【解析】试题分析:由向量的三角形法则,.考点:平行四边形法则,三角形法则.2.设是两个单位向量,则下列结论中正确的是( )A. B. C. D. 【答案】D【解析】【分析】根据单位向量的概念,可直接得出结果.【详解】单位向量即是模为 1 的向量;若是两个单位向量,则.故选 D【点睛】本题主要考查单位向量,熟记概念即可,属于基础题型.3.向量化简后等于( )A. B. C. D. 【答案】C【解析】,选 C.4.等边中,向量的夹角为( )A. B. C. D. 【答案】D【解析】试题分析:如图,由向量夹角的定义,要把向量移到同一起点,故三角形的内角 ABC,并非向量的夹角,需把向量平移到,此时所夹的∠CBD 才是向量的夹角,由邻补角的关系可得∠CBD=180°-∠ABC=120°故答案为:120°.考点:数量积表示两个向量的夹角.5.已知且,则 点的坐标为( )A. B. C. D. 【答案】C【解析】【分析】设 点的坐标为,根据题意得到与的坐标,由,即可得出结果.【详解】设 点的坐标为,因为,所以,,因为,所以,因此,解得,即.故选 C【点睛】本题主要考查向量的坐标运算,熟记运算法则即可,属于基础题型.6.在中, 已知分别为的三个内角所对的边,其中,则角 的度数为( )A. B. C. D. 【答案】C【解析】【分析】根据正弦定理先求出,再由,即可得出结果.【详解】因为,由正弦定理可得:,解得,因为,所以,因此.故选 C【点睛】本题主要考查解三角形,熟记正弦定理即可,属于基础题型.7.已知向量 和 的夹角为,,则( ).A. B. C. 4D. 【答案】D【解析】试题分析:因为向量 和 的夹角为 1200,,所以.考点:平面向量的模长公式.8.在中,已知 是边上一点,,,则 等于( )A. B. C. D. 【答案】A【解析】【分析】利用向量的减法将3,进行分解,然后根据条件λ,进行对比即可得到结论【详解】 3,∴33,即 43,则, λ,∴λ,故选:B.【点睛】本题主要考查向量的基本定理的应用,根据向量的减法法则进行分解是解决本题的关键.9.已知向量满足,且 在 方向上的投影与 在 方向上的投影相等,则等于( )A. 1B. C. D. 3【答案】C【解析】【分析】先设向量的夹角为 ,根据 在 方向上的投影与 在 方向上的投影相等,求出,再由即可求出...