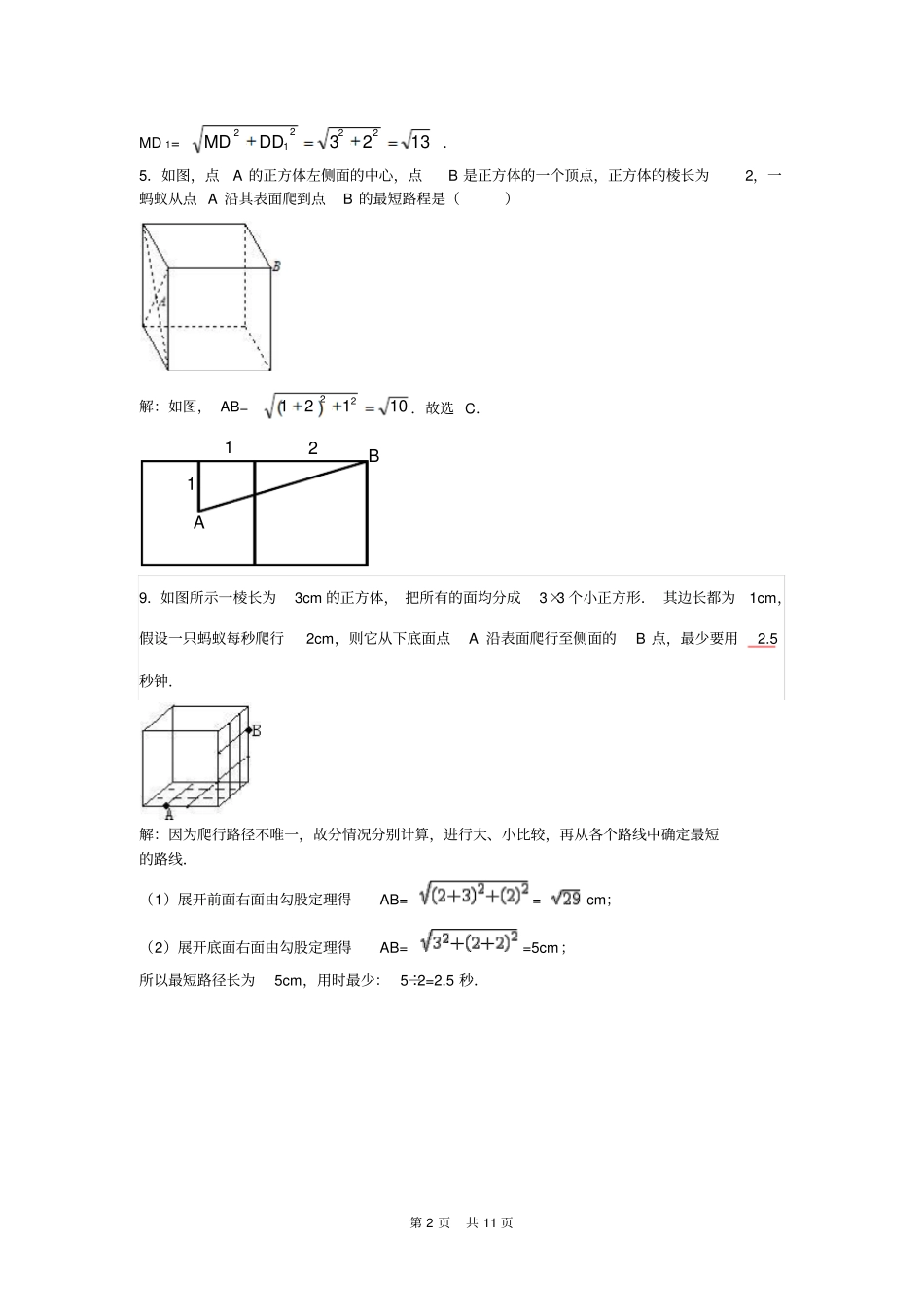
第 1 页共 11 页蚂蚁爬行的最短路径正方体4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处, 它爬行的最短路线是()A.A? P? B B.A ? Q? B C.A? R? B D.A? S? B 解:根据两点之间线段最短可知选A.故选 A .2. 如图,边长为1 的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是. 解:如图将正方体展开,根据“两点之间,线段最短”知,线段 AB 即为最短路线.AB= 51222.8. 正方体盒子的棱长为2, BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为. 解:将正方体展开,连接M 、D1,根据两点之间线段最短,MD=MC+CD=1+2=3 ,第 6 题第 7 题第 2 页共 11 页MD 1=132322212DDMD.5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点 A 沿其表面爬到点B 的最短路程是()解:如图, AB=1012122.故选 C.AB1219.如图所示一棱长为3cm 的正方体, 把所有的面均分成3×3 个小正方形. 其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm;(2)展开底面右面由勾股定理得AB= =5cm;所以最短路径长为5cm,用时最少: 5÷2=2.5 秒.第 3 页共 11 页ABA1B1DCD1C1214长方体10.(2009?恩施州)如图,长方体的长为15,宽为 10,高为 20,点 B 离点 C 的距离为 5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点 B,需要爬行的最短距离是。解:将长方体展开,连接A、B,根据两点之间线段最短,AB= =25.11. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C1 处(三条棱长如图所示) ,问怎样走路线最短?最短路线长为. 解:正面和上面沿A 1B 1 展开如图,连接AC 1,△ABC 1 是直角三角形,∴AC 1=5342142222212BCAB18.( 2011?荆州)如图,长方体的底面边长分别为2cm 和 4cm,高为 5cm.若一只蚂蚁从P 点开始经过4 个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为cm.第 4 页共 11 页解: PA=2×(4+2)=12,QA=5 ∴PQ=13.故答案为: 13.19.如图,一块长方体砖宽AN=5cm ,长 ND=10cm ,CD 上的点 B 距地面的高BD=8cm ,地面上 ...