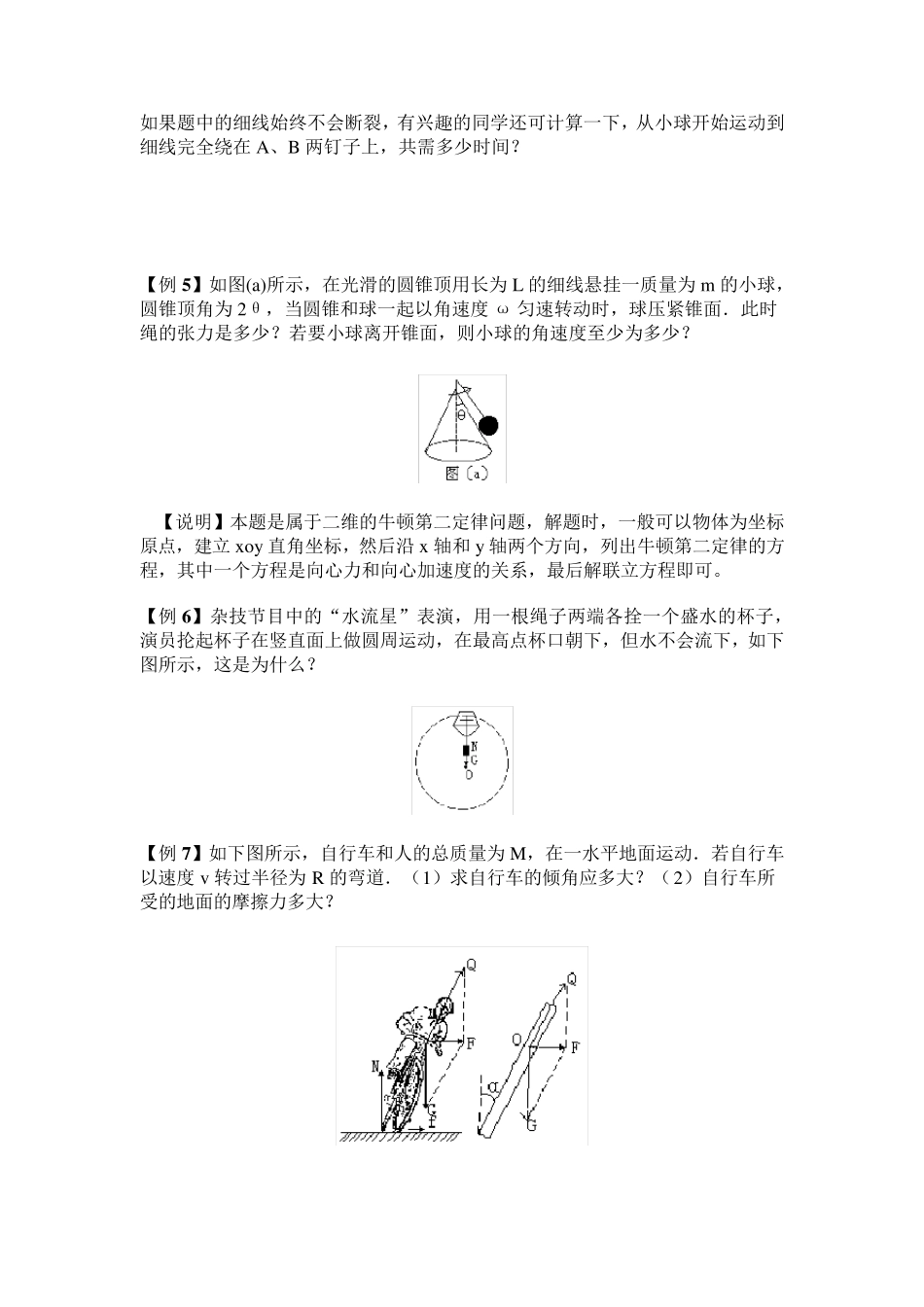
“匀速圆周运动”的典型例题 【例 1 】如图所示的传动装置中,A、B 两轮同轴转动.A、B、C 三轮的半径大小的关系是 RA=RC=2RB.当皮带不打滑时,三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少? 【例 2 】一圆盘可绕一通过圆盘中心 O 且垂直于盘面的竖直轴转动.在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动(见图),那么 [ ] A.木块受到圆盘对它的摩擦力,方向背离圆盘中心 B.木块受到圆盘对它的摩擦力,方向指向圆盘中心 C.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同 D.因为摩擦力总是阻碍物体运动,所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反 E.因为二者是相对静止的,圆盘与木块之间无摩擦力 【例3】在一个水平转台上放有A、B、C 三个物体,它们跟台面间的摩擦因数相同.A 的质量为2m,B、C 各为m.A、B 离转轴均为r,C 为2r.则 [ ] A.若 A、B、C 三物体随转台一起转动未发生滑动,A、C 的向心加速度比 B 大 B.若 A、B、C 三物体随转台一起转动未发生滑动,B 所受的静摩擦力最小 C.当转台转速增加时,C 最先发生滑动 D.当转台转速继续增加时,A 比 B 先滑动 【例4】如图,光滑的水平桌面上钉有两枚铁钉 A、B,相距 L0=0.1m.长 L=1m的柔软细线一端拴在A 上,另一端拴住一个质量为500g 的小球.小球的初始位置在AB 连线上A 的一侧.把细线拉直,给小球以2m/s 的垂直细线方向的水平速度,使它做圆周运动.由于钉子 B 的存在,使细线逐步缠在A、B 上. 若细线能承受的最大张力Tm=7N,则从开始运动到细线断裂历时多长? 【说明】圆周运动的显著特点是它的周期性.通过对运动规律的研究,用递推法则写出解答结果 的通式 ( 一般 表 达 式 ) 有很 重 要 的意 义 .对本 题 ,还 应 该 熟 练 掌握 数列 求 和 方法. 如果题中的细线始终不会断裂,有兴趣的同学还可计算一下,从小球开始运动到细线完全绕在A、B 两钉子上,共需多少时间? 【例5 】如图(a)所示,在光滑的圆锥顶用长为L 的细线悬挂一质量为m 的小球,圆锥顶角为2θ,当圆锥和球一起以角速度 ω 匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少? 【说明】本题是属于二维的牛顿第二定律问题,解题时,一般可以物体为坐标原...