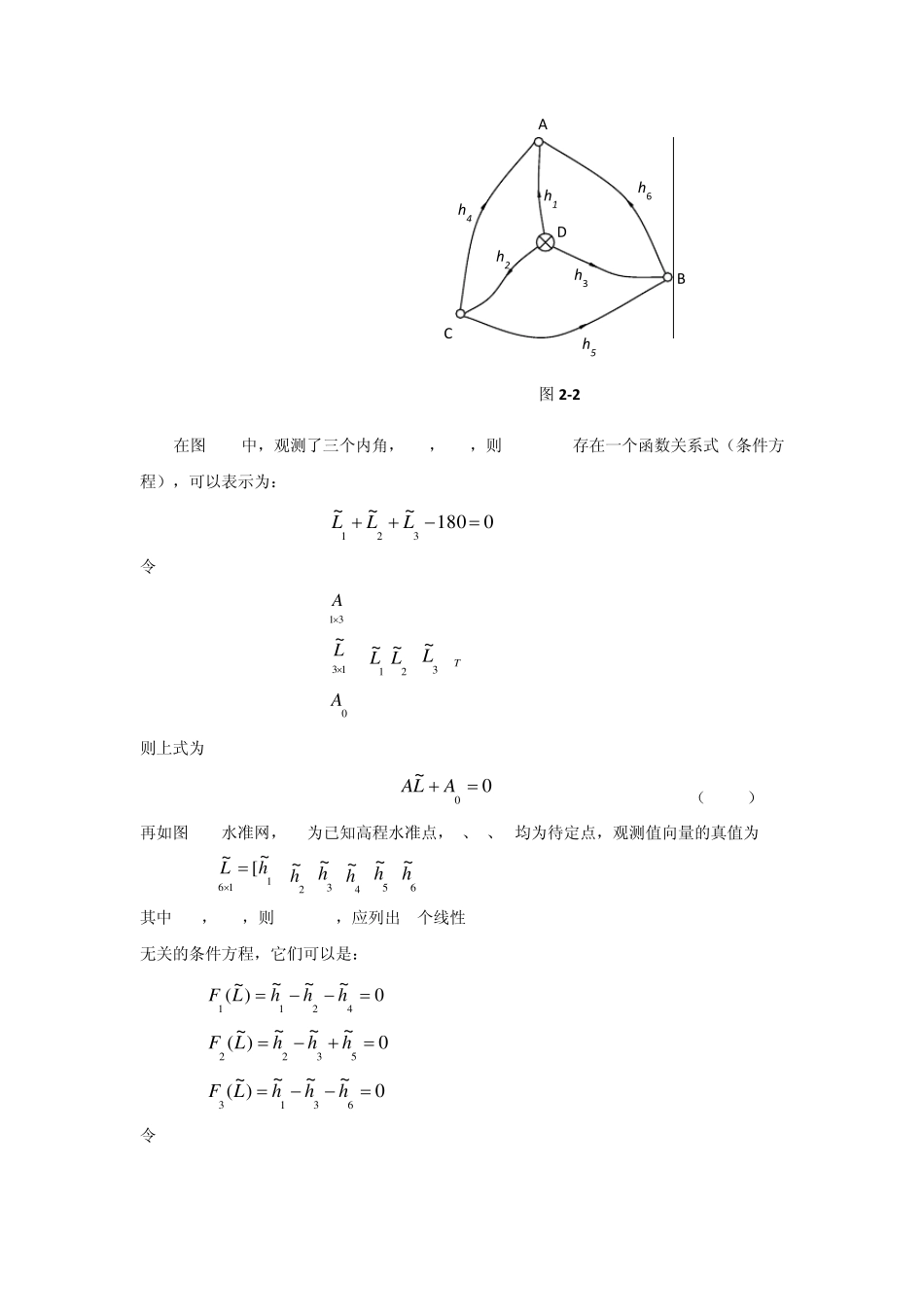
本节重点:(1)测量平差的函数模型定义,类型;测量平差的数学模型包括:条件平差法模型、间接平差法模型、附有参数的条件平差法模型、附有限制条件的间接平差法模型、综合平差模型; (2)测量平差的随机模型。 本节教学思路: 首先说明平差的数学模型分两类:函数模型与随机模型,进而分别阐述其定义、分类及建立的方法和模型的具体形态。 教学内容: 一、平差模型的定义与分类 1.从模型的性质分:函数模型、随机模型,函数模型连同随机模型称平差的数学模型; 2.函数模型又分为:条件平差法模型、间接平差法模型、附有参数的条件平差法模型、附有限制条件的间接平差法模型、综合平差模型; 二、各类函数模型的建立 (一)概述 1.函数模型定义: 在科学技术领域,通常对研究对象进行抽象概括,用数学关系式来描述它的某种特征或内在的联系,这种数学关系式就称为函数模型。 2.函数模型的意义与特点 函数模型是描述观测量与待求量之间的数学函数关系的模型。 对于一个平差问题,建立函数模型是测量平差中最基本、最重要的问题,模型的建立方法不同,与之相应就产生了不同的平差方法。 函数模型有线性与非线性之分,测量平差通常是基于线性函数模型,当函数模型为非线性时(如(2-1-4)式),总是要将其线性化。 (二)各种经典平差方法及其线性函数模型的建立方法。 1. 条件平差法及其函数模型 首先通过两个例子,来说明条件平差函数模型的建立方法。 在图2-1中,观测了三个内角,n=3,t=2,则r=n-t=1,存在一个函数关系式(条件方程),可以表示为: 令 =[1 1 1] =[ ] =[-180] 则上式为 (2-2-1) 再如图2-2水准网, D为已知高程水准点,A、B、C均为待定点,观测值向量的真值为 ] 其中n=6,t=3,则r=n-t=3,应列出 3个线性 无关的条件方程,它们可以是: 令 0180~~~321LLL31A13~L1~L2~L3~LT0A0~0 ALA116~[~hL 2~h3~h4~h5~h6~h0~~~)~(4211hhhLF0~~~)~(5322hhhLF0~~~)~(6313hhhLF 图2 -2 D h1 h2 h3 h5 h4 h6 A B C 则上面条件方程组可写为 (2-2-2) 一般而言,如果有n个观测值,必要观测个数为t,则应列出r=n-t个条件方程,即 (2-2-3) 如果条件方程为线性形式,则可以直接写为 (2-2-4) 将代入(2-2-4)式,并令 (2-2-5) 则(2-2-4)式为 (2-2-6) (2-2-4)或(2-2-6)式即为条件平差的函数模型。以此模型为基础的平差...