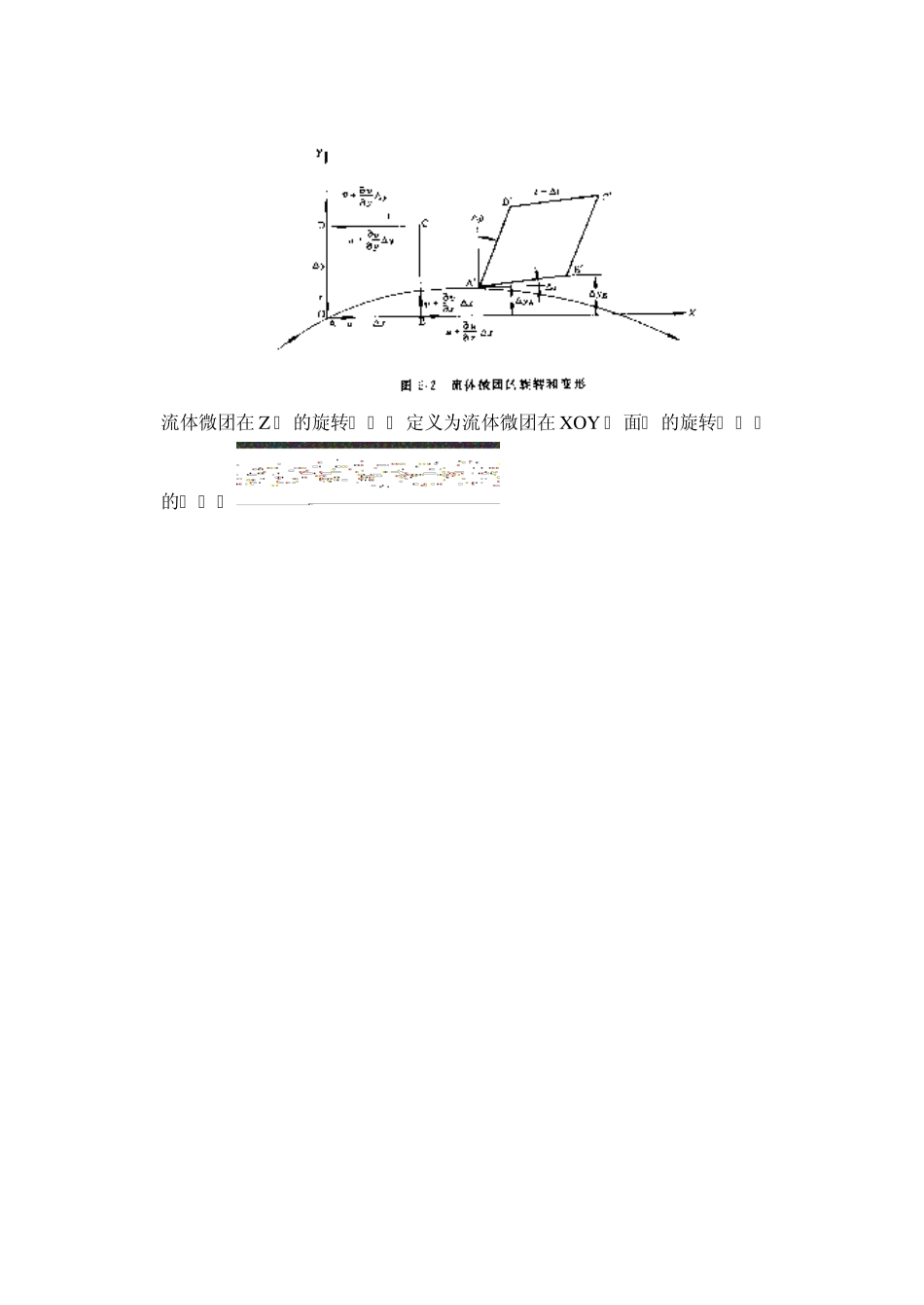
第五章 不可压缩流体的二维流动 引言:在前面几章主要讨论了理想流体和黏性流体一维流动,为解决工程实际中存在的一维流动问题打下了良好的基础。本章讨论理想不可压流体的二维有势流动以及二维黏性流体绕物体流动的基本概念。 第一节 有旋流动和无旋流动 刚体的运动可分解为移动和转动两种运动形式, 流体具有移动和转动两种运动形式。另外,由于流体具有流动性,它还具有与刚体不同的另外一种运动形式,即变形运动(deformationmotion)。本节只介绍流体旋转运动即有旋流动(rotation—alflow)和无旋流动(irrotational flow)。 一、有旋流动和无旋流动的定义 流体的流动是有旋还是无旋,是由流体微团本身是否旋转来决定的。流体在流动中,如果流场中有若干处流体微团具有绕通过其自身轴线的旋转运动,则称为有旋流动,如果在整个流场中各处的流体微团均不绕自身轴线的旋转运动,则称为无旋流动。 强调“判断流体流动是有旋流动还是无旋流动,仅仅由流体微团本身是否绕自身轴线的旋转运动来决定,而与流体微团的运动轨迹无关。” 举例虽然流体微团运动轨迹是圆形,但由于微团本身不旋转,故它是无旋流动;在图 5—1(b)中,虽然流体微团运动轨迹是直线,但微团绕自身轴线旋转,故它是有旋流动。在日常生活中也有类似的例子,例如儿童玩的活动转椅,当转轮绕水平轴旋转时,每个儿童坐的椅子都绕水平轴作圆周运动,但是每个儿童始终是头向上,脸朝着一个方向,即儿童对地来说没有旋转。 二、旋转角速度(rotationalangularvelocity) 为了简化讨论,先分析流体微团的平面运动。如图 5—2 所示有一矩形流体微团 ABCD 在 XOY 平面内,经丛时间后沿一条流线运动到另一位置,微团变形成 A,B,C,D。 流体微团在 Z周的旋转角速度定义为流体微团在 XOY 平面上的旋转角速度的平均值 速度环量是一个标量,但具有正负号。 速度环量的正负号与速度方向和积分时所取的绕行方向有关。后者一般规定为:当沿封闭曲线 K 反时针方向绕行时,取为正号。 二、旋涡强度(strength Of v ortex ) 沿封闭曲线 K 的速度环量与有旋流动之间有一个重要的关系。 如图 5—5 所示,在平面 XOY 上取一微元矩形封闭曲线,其面积 dA=dx dy ,沿封闭曲线反时针方向 ABCDA 的速度环量推导 得是沿任何封闭曲线的速度环量 都等于零,则在这区域内的流动一定是无旋流动。 (例 5—2 ) 一个以角速度ω按反时针方向作像刚体一样旋转的流动...