完整版试验5最小生成树算法的设计与实现报告VIP专享VIP免费

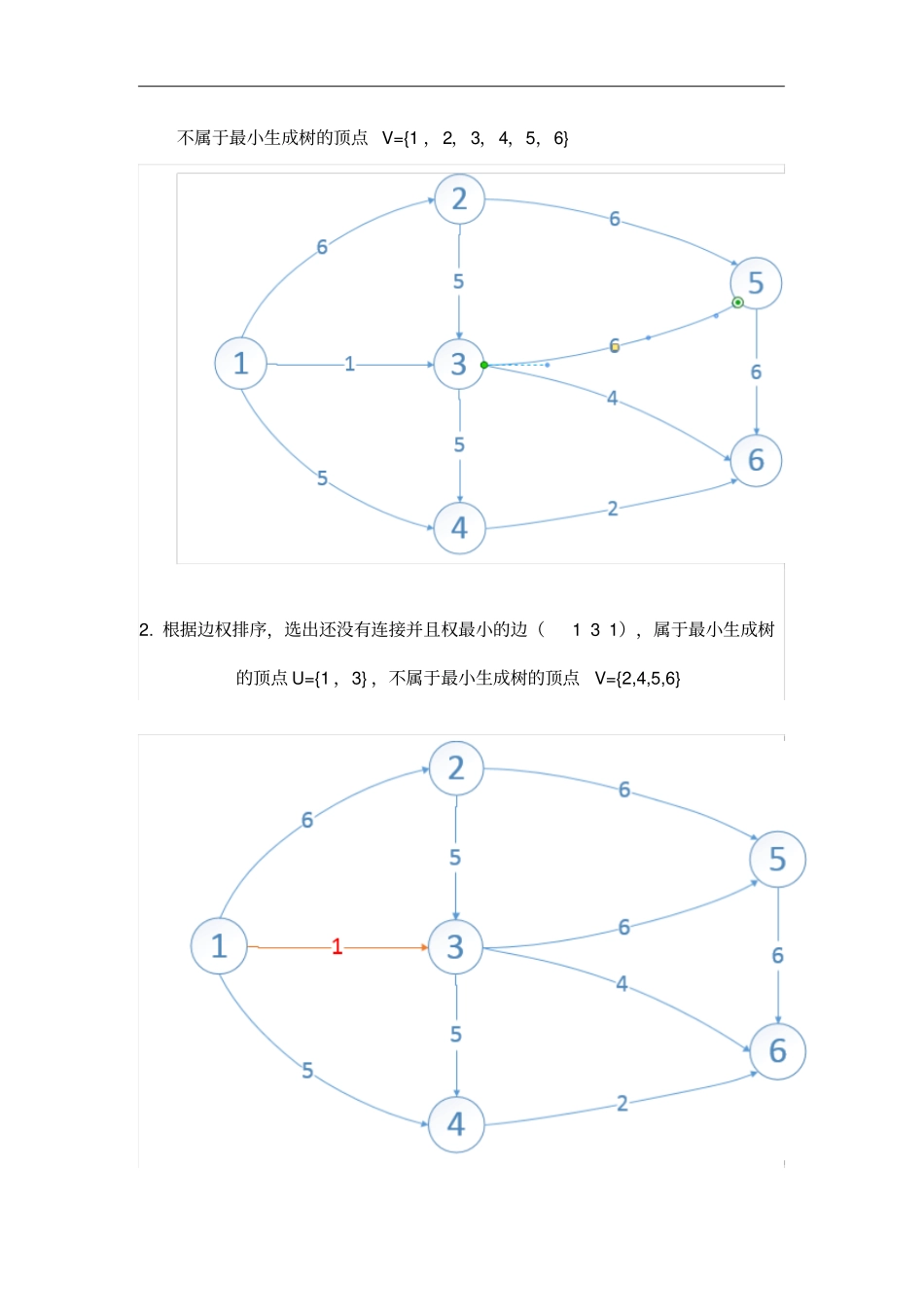
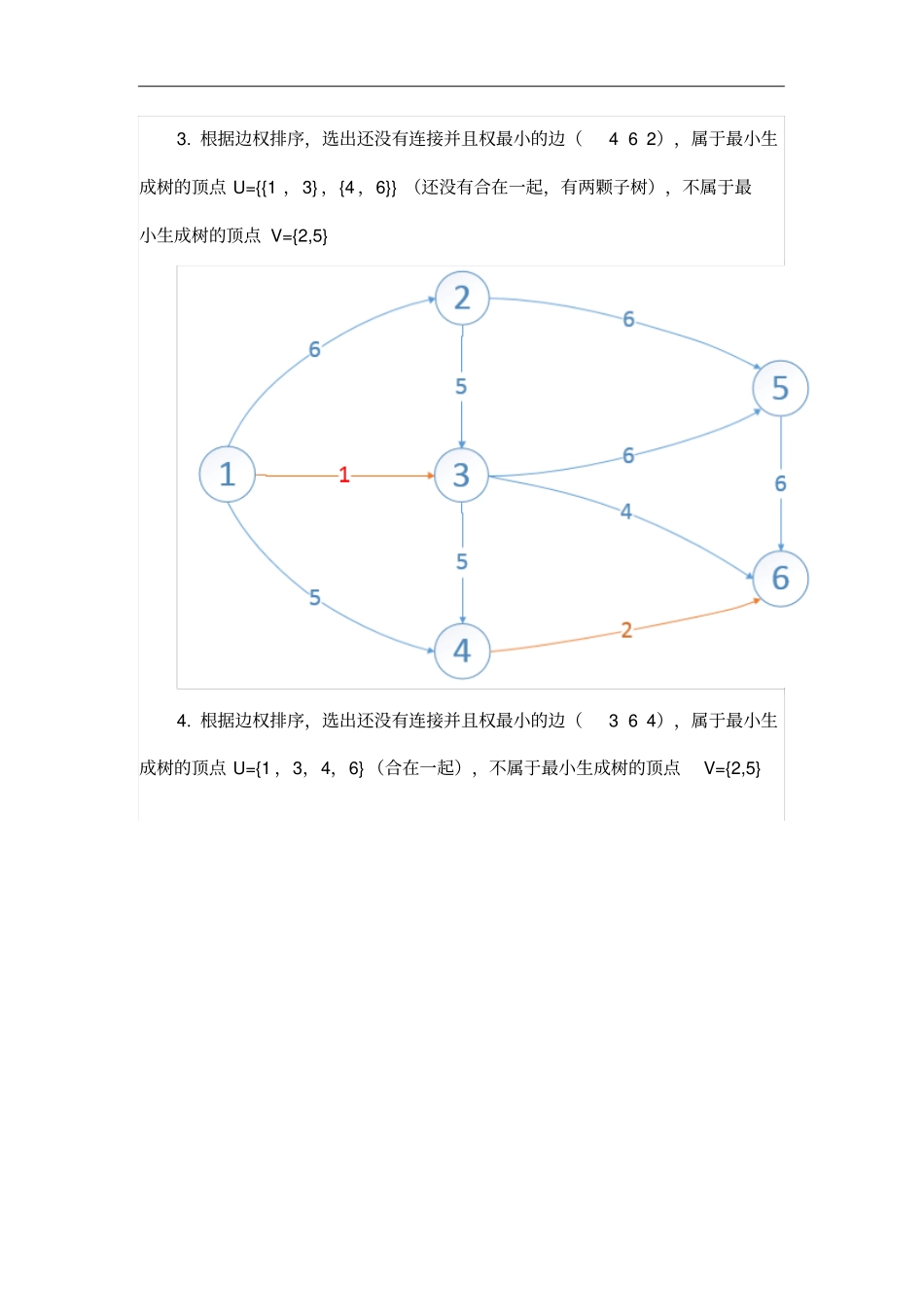
实验 5 最小生成树算法的设计与实现一、实验目的1、根据算法设计需要 , 掌握连通图的灵活表示方法；2、掌握最小生成树算法，如Prim、Kruskal算法；3、基本掌握贪心算法的一般设计方法；4、进一步掌握集合的表示与操作算法的应用。二、实验内容1、认真阅读算法设计教材和数据结构教材内容, 熟习连通图的不同表示方法和最小生成树算法；2、设计 Kruskal算法实验程序。有n个城市可以用（ n-1）条路将它们连通，求最小总路程的和。设计测试问题 ,修改并调试程序 , 输出最小生成树的各条边, 直至正确为止。三、Kruskal 算法的原理方法边权排序 : 1 3 1 4 6 2 3 6 4 1 4 5 2 3 5 3 4 5 2 5 6 1 2 6 3 5 6 5 6 6 1. 初始化时：属于最小生成树的顶点U={} 不属于最小生成树的顶点 V={1 ，2，3，4，5，6} 2. 根据边权排序，选出还没有连接并且权最小的边（1 3 1），属于最小生成树的顶点 U={1 ，3} ，不属于最小生成树的顶点V={2,4,5,6} 3. 根据边权排序，选出还没有连接并且权最小的边（4 6 2），属于最小生成树的顶点 U={{1 ，3} ，{4 ，6}} （还没有合在一起，有两颗子树），不属于最小生成树的顶点 V={2,5} 4. 根据边权排序，选出还没有连接并且权最小的边（3 6 4），属于最小生成树的顶点 U={1 ，3，4，6} （合在一起），不属于最小生成树的顶点V={2,5} 5. 根据边权排序，选出还没有连接并且权最小的边（3 6 4），属于最小生成树的顶点 U={1 ，2，3，4，6}, ，不属于最小生成树的顶点V={5} 6. 根据边权排序，选出还没有连接并且权最小的边（3 6 4），属于最小生成树的顶点 U={1 ，2，3，4，5，6} 此时，最小生成树已完成四、实验程序的功能模块功能模块：bool cmp(Edge a,Edge b)； //定义比较方法int getfa(int x)；//在并查集森林中找到x 的祖先int same(int x,int y)；//判断祖先是否是同一个，即是否联通void merge(int x,int y); //合并子树，即联通两子树sort(e+1,e+m+1,cmp); //对边按边权进行升序排序详细代码：#include #include #include #include #define MAXN_E 100000 #define MAXN_V 100000 using namespace std; struct Edge{ int fm,to,dist; //边的起始顶点，边的到达顶点，边权}e[MAXN_E]; int fa[MAXN_V],n,m; //顶点数组，顶点总数，边总数//定义比较，...