中考数学重要公式(全归纳)VIP免费

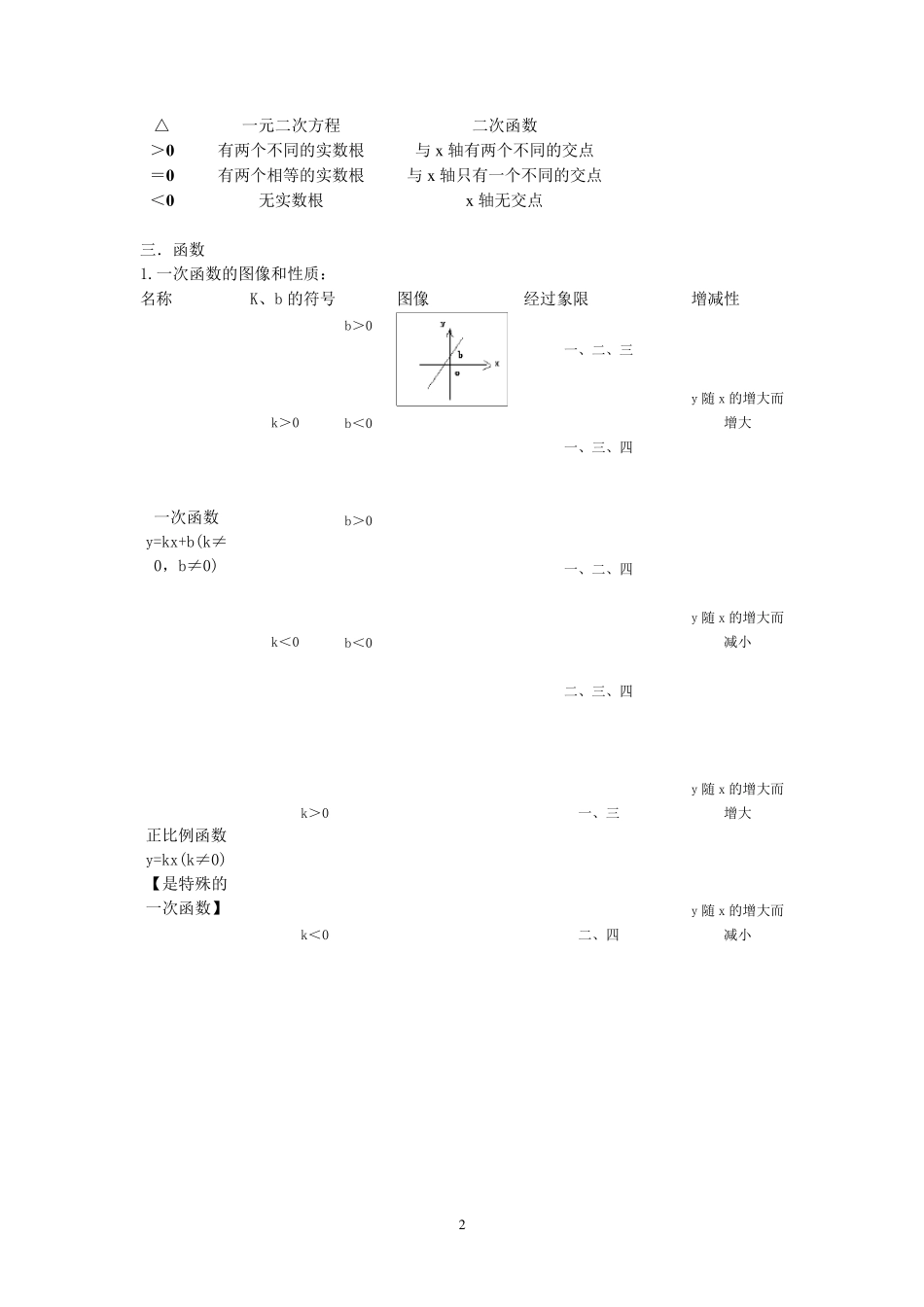
1 重要公式 代数部分 一．数与式 1. |a|a 2  2.)0()(2aaa 3.aa 33 4.)0(1为正整数，paaapp,特别地，）（011aaa 5.)0(10aa 6.)(11-为奇数）（nn =为偶数）（n1 2.分母有理化 ①)0( ＞aaabab  ②)00())(()(＞，＞bababmambababambam 3.非负数的算术平方根 例：9 的算术平方根是3 4.（1）①分式有意义，分母不为0,例如：要使1342 xx有意义，则1x； ②如果分子分母中有开平方，则分子根号下的式子必须≥0，分母根号下的式子必须＞0， 例如：要使 42123xx有意义，则3x+12≥0 解得 x＞2 2x-4＞0 （2）要使分式值为0，必须保证分子为0 的同时分母不为0. 例如： 1322xxx的值为0，则010322xxx同时必须使，解得 x=3 二．一元二次方程 1.一元二次方程)0(2acbxax求根公式： ）（△042422acbaacbbx 2.根与系数的关系（韦达定理）： 若一元二次方程)0(2acbxax的两根分别为21xx、，则 abxx21 acxx21 3.△的作用 2 △ 一元二次方程 二次函数 ＞0 有两个不同的实数根 与x 轴有两个不同的交点 ＝0 有两个相等的实数根 与x 轴只有一个不同的交点 ＜0 无实数根 x 轴无交点 三．函数 1.一次函数的图像和性质： 名称 K、b 的符号 图像 经过象限 增减性 一次函数y=kx+b(k≠0，b≠0) k＞0 b＞0 一、二、三 y 随 x 的增大而增大 b＜0 一、三、四 k＜0 b＞0 一、二、四 y 随 x 的增大而减小 b＜0 二、三、四 正比例函数y=kx(k≠0) 【是特殊的一次函数】 k＞0 一、三 y 随 x 的增大而增大 k＜0 二、四 y 随 x 的增大而减小 3 2.（1）反比例函数的图像和性质 反比例函数 )0(kxky k 的符号 k>0 k<0 图像 性质 ①x 的取值范围是x 0， y 的取值范围是y 0； ②当k>0 时，函数图象的两个分支分别在第一、三象限。在每个象限内，y 随x 的增大而减小. ①x 的取值范围是x 0， y 的取值范围是y 0； ②当k<0 时，函数图象的两个分支分别在第二、四象限。在每个象限内，y 随x 的增大而增大. 对称性 ①)0(kxky的图象是轴对称图形，对称轴为)0( ＞kxy 或)0( ＜kxy ②)0(kxky的图象是中心对称图形，对称中心为原点（0，0）； ③xkyxky和 (k≠0)在同一坐标系中的图象关于 x轴对称，也关于 y轴...