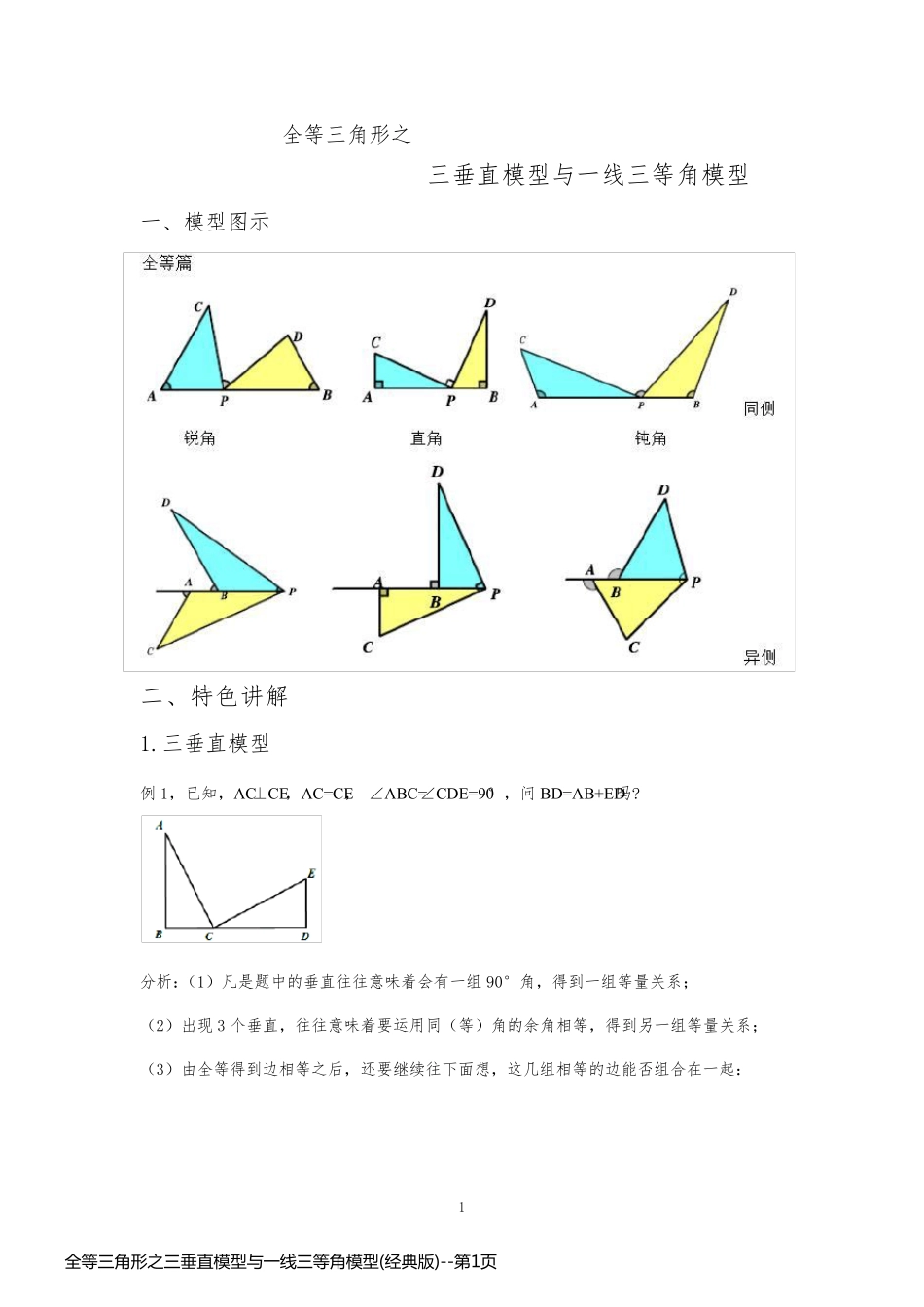
1 全等三角形之 三垂直模型与一线三等角模型 一、模型图示 二、特色讲解 1.三垂直模型 例1,已知,AC⊥CE,AC=CE, ∠ABC=∠CDE=90°,问 BD=AB+ED吗? 分析:(1)凡是题中的垂直往往意味着会有一组 90°角,得到一组等量关系; (2)出现 3 个垂直,往往意味着要运用同(等)角的余角相等,得到另一组等量关系; (3)由全等得到边相等之后,还要继续往下面想,这几组相等的边能否组合在一起: 全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 1页全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 1页2 练习1:如图, 如果△ABC≌△CDE,请说明AC与CE的关系。 提示:线段的关系包括:大小关系与位置关系 练习2:如图,E是正方形ABCD的边DC上的一点,过点A作FA⊥AE交CB的延长线于点F, 求证:DE=BF 练习3:如图,在△ABC中,∠BAC=90°,AB=AC,AE是过点A的直线,BD⊥AE,CE⊥AE,如果CE=3,BD=7,请你求出 DE的长度。 全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 2页全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 2页3 练习4:在△ABC中,∠ACB= 900,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。 (1)当直线MN绕点C旋转到图9 的位置时,△ADC≌△CEB,且 DE=AD+BE。你能说出其中的道理吗? (2)当直线MN绕点C旋转到图10 的位置时, DE =AD-BE。说说你的理由。 (3)当直线MN 绕点C 旋转到图11 的位置时,试问 DE,AD,BE 具有怎样的等量关系?请写出这个等量关系。 图11 EDCBANM图12 EDCBANMEDCBANM图10 全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 3页全 等 三 角 形 之 三 垂 直 模 型 与 一 线 三 等 角 模 型 (经 典 版 )--第 3页4 2.一线三等角模型 例2:如图,已知△ABC为等边三角形,D、E、F 分别在边BC、CA、AB上,且△DEF也是等边三角形。 (1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的; (2)你所证明相等的线段,可以通过怎样的变化想到得到?写出变化过程。 练习1.如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E、F分别是直线CD上两点,且...