正态分布课件VIP免费

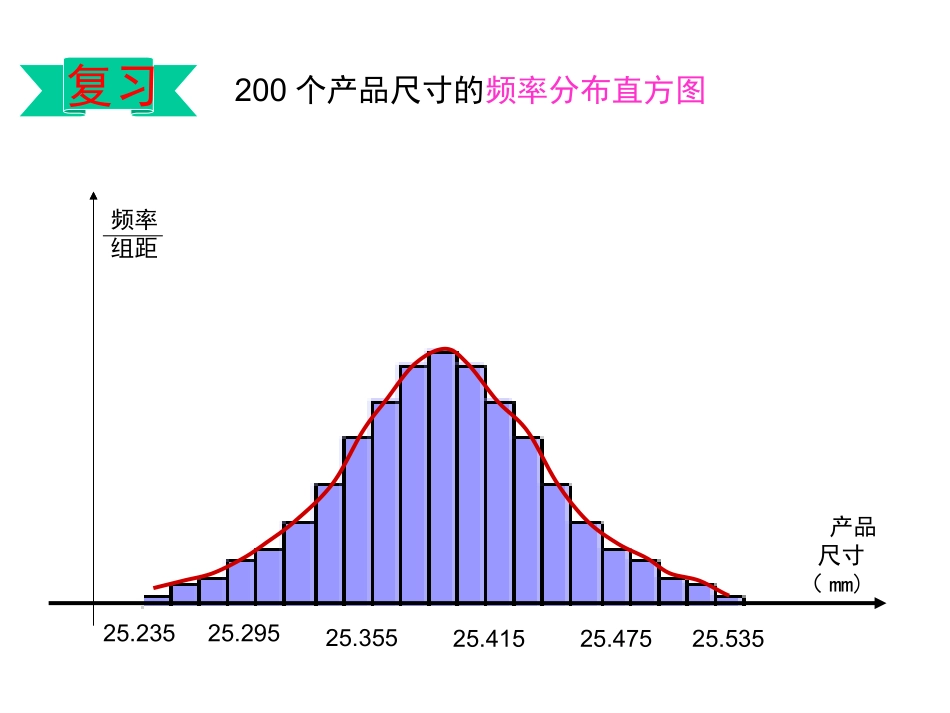
高二数学选修2-3复习100个产品尺寸的频率分布直方图25.23525.29525.35525.41525.47525.535产品尺寸（mm)频率组距“面积”频率·25.23525.29525.35525.41525.47525.535产品尺寸（mm)频率组距复习200个产品尺寸的频率分布直方图复习样本容量无限增大时频率组距产品尺寸(mm)总体密度曲线“面积”概率·ab样本总体频率概率总体密度曲线与x轴之间的面积等于多少？1高尔顿板导入点击演示11总体密度曲线钟形线y0x1定义：频率组距正态曲线),(x函数22()21()2xxe式中的实数μ、σ(σ>0)是参数，称的图象称为正态曲线xx0若用X表示落下的小球第1次与数轴接触时的坐标,则X是一个随机变量，X是离散型随机变量吗？abX0连续型随机变量X落在区间(a,b]的概率与其总体密度曲线（正态曲线）有何关系？这部分面积如何计算？()=PaXb,()baxdxY22()212xxe，2.正态分布的定义:如果对于任何实数a0）（5）正态曲线与x轴之间的面积是1σ的值一定时，μ的值对正态曲线影响σ=0.50yxμ=11μ=-1-1μ=022(1)22xxe1，0.522(1)22xxe-1，0.5当σ一定时,曲线随着μ的变化而沿x轴平移μ是总体的均值。μ的值一定时，σ的值对正态曲线的影响=0.5=1=2μ=0y0x当μ一定时,曲线的形状由σ确定σ越小,曲线越“瘦高”,表示总体的分布越集中，σ越大,曲线越“矮胖”表示总体的分布越分散。σ代表总体的标准差σ2代表总体的方差正态曲线下的面积规律S(-,-a)S(+a,)＝S(-,-a)-a+a正态曲线下的面积规律•关于直线x=对称的两区域面积相等。•关于直线x=对称的两区间上的概率相等。S(-x1,-x2)-x1-x2+x2+x1S(+x1,+x2)=S(-x2,-x1)区间概率（μ－σ，μ＋σ]68.27%（μ－2σ，μ＋2σ]95.44%（μ－3σ，μ＋3σ]99.73%通常认为若X~N（μ，σ2），则X只在（μ－3σ，μ＋3σ]内取值，在此区间外取值是小概率事件，几乎不可能发生。“3σ原则”某镇农民的年平均收入服从正态分布N(5000,2002),试求该镇农民年平均收入在范围内的概率.(5000,5200](5000,5400](5200,5400]区间概率(μ－σ,μ＋σ)68.27%(μ－2σ,μ＋2σ)95.44%(μ－3σ,μ＋3σ)99.73%(4800,5200]48005200540068.27%47.72%-34.135%=13.585%95.44%÷2=47.72%68.27%÷2=34.135%(-∞,4600](1-95.44%)÷2=2.28%课堂小结:22()21()2xxe频率组距x随机变量X满足:,()=()baPaXbxdx则称X服从正态分布.记作：X~N（μ，σ2）一、正态曲线及其解析式二、正态分布三、正态分布的“3σ原则”课堂小结:XOY四、正态曲线的特征(1)曲线在x轴上方,与x轴不相交；(2)曲线是单峰的,它关于直线x=μ对称；(3)曲线在x=μ处达到峰值；(4)曲线与x轴之间的面积为１；(5)当σ一定时,曲线的水平位置由μ确定。随着μ的变化而沿x轴平移；μ为总体的均值(6)当μ一定时,曲线的形状由σ确定.σ越小,曲线越“瘦高”,σ越大,曲线越“矮胖”,σ为总体的标准差。(7)对称区域面积相等21x=μ