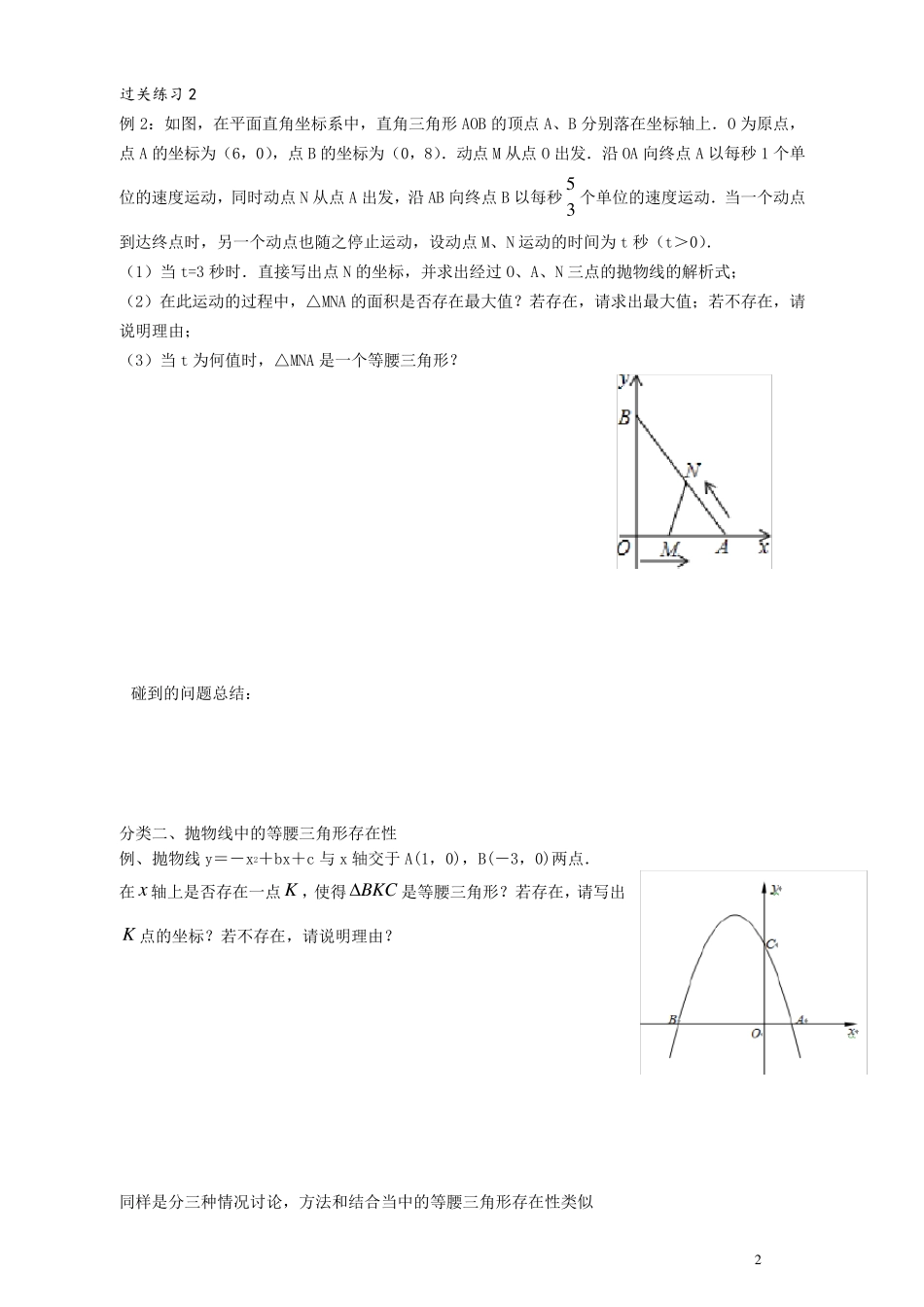
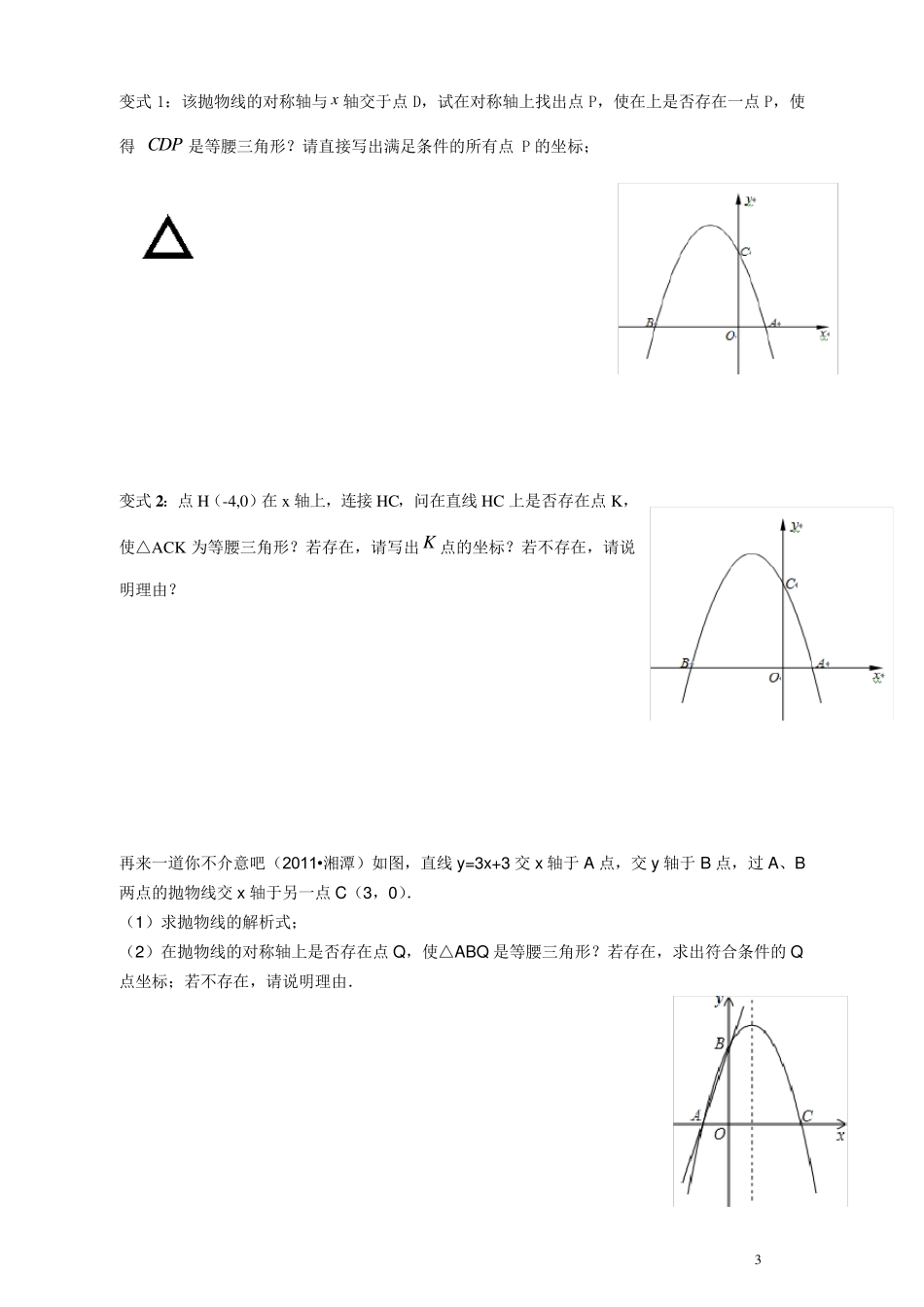
1 等腰三角形的存在性 一、 等腰三角形存在性 分类一、几何动点中等腰三角形存在性 如图,在梯形ABCD 中,35424 5ADBCADDCABB∥,,,,∠.动点M 从 B 点出发沿线段 BC 以每秒 2 个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒 1 个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1 )求 BC 的长.(2 )当 MNAB∥时,求t 的值. (3 )试探究:t 为何值时,MNC△为等腰三角形. 方法:动点问题,养成把可以用未知数表示的边都用未知数表示 等腰三角形存在性,一般可以分三种情况 要求 t 的值,通常情况下用等腰三角形的三线合一性质做高,然后利用相似列式子 过关练习 1 (本小题满分9 分)如图所示,在平面直角坐标系中,四边形OABC 是等腰梯形,BCOA∥,746 0OAABCOA,,∠,点P 为 x 轴上的一个动点,点P 不与点O 、点A 重合.连结CP ,过点P 作 PD 交 AB 于点D . (1 )求点B 的坐标; (2 )当点P 运动什么位置时,OCP△为等腰三角形,求这时点P 的坐标; (3 )当点P 运动什么位置时,使得CPDOAB∠∠,且58BDAB ,求这时点P 的坐标. A D C B M N (第 2 3 题ABCODPxy 2 过关练习2 例2:如图,在平面直角坐标系中,直角三角形AOB 的顶点A、B 分别落在坐标轴上.O 为原点,点A 的坐标为(6,0),点B 的坐标为(0,8).动点M 从点O 出发.沿OA 向终点A 以每秒1 个单位的速度运动,同时动点N 从点A 出发,沿AB 向终点B 以每秒35个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N 运动的时间为t 秒(t>0). (1)当t=3 秒时.直接写出点N 的坐标,并求出经过O、A、N 三点的抛物线的解析式; (2)在此运动的过程中,△MNA 的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由; (3)当t 为何值时,△MNA 是一个等腰三角形? 分类二、抛物线中的等腰三角形存在性 例、抛物线y=-x2+bx+c 与 x 轴交于 A(1,0),B(-3,0)两点. 在x轴上是否存在一点K ,使得 BKC是等腰三角形?若存在,请写出K 点的坐标?若不存在,请说明理由? 同样是分三种情况讨论,方法和结合当中的等腰三角形存在性类似 碰到的问题总结: 3 变式1:该抛物线的对称轴与x轴交于点D,试在对称轴上找出点P,使在上是否存在一点P,使得CDP ...