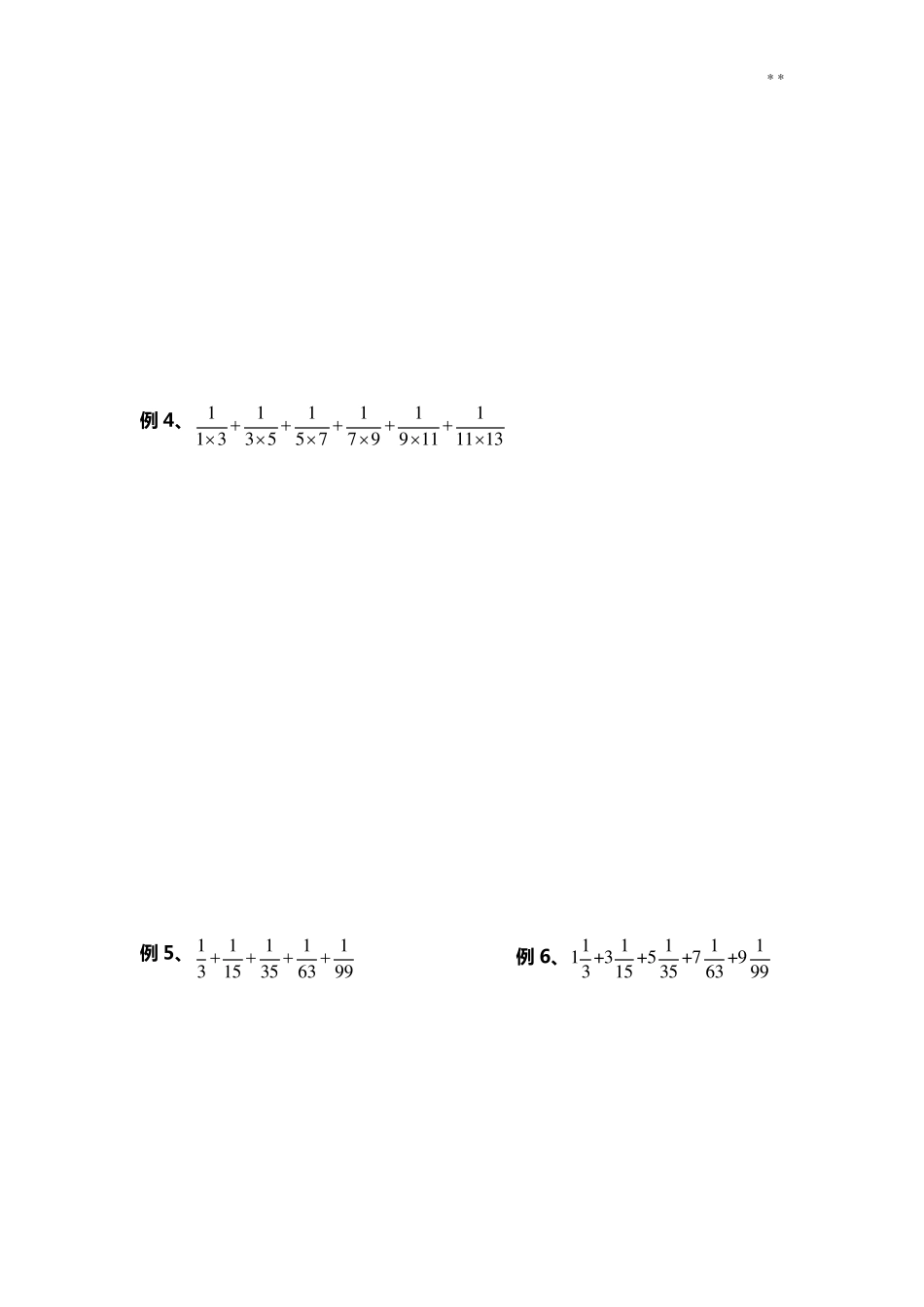
* * 第 5 讲 简 便 计 算 ( 四 ) —— 列 项 相 消 法 ( 拆 分 法 ) 一:裂项 相 消 法 ( 拆 分 法 ) : 把 一 个 分 数 拆 成 两 个 或 两 个 以 上 分 数 相 减 或 相 加 的 形 式 , 然 后 再 进 行 计 算 的 方 法 叫 做 裂 项 相 消 法 , 也 叫 拆 分 法 。 二:列 项 相 消 公式 ( 1)111(n1)1nnn ( 2)11kn nknnk ( 3)1111()(n)nknnkk ( 4) 1111121122n nnn nnn ( 5)11aba bab ( 6)22abbaa bab 三:数列 ( 1) 定 义 : 按 一 定 的 次 序 排 列 的 一 列 数 叫 做 数 列 。 (2)数 列 中 的 每 一 个 数 叫 做 这 个 数 列 的 项 。 依 次 叫 做 这 个 数 列 的 第 一 项 ( 首 项 )、第 二 项 、、、、、、第 n 项 ( 末 项 )。 ( 3) 项 数 : 一 个 数 列 中 有 几 个 数 字 , 项 数 就 是 几 。 四 :等差数列 ( 1) 定 义 : 如 果 一 个 数 列 从 第 二 项 起 , 每 一 项 与 它 的 前 一 项 的 差 等 于 同 一 个 常 数 , 这个 数 列 就 叫 做 等差数列 。 而 这 个 常 数 叫 做 等 差 数 列 的 公差。 ( 2) 等 差 数 列 的 和=( 首 项 +末 项 ) × 项 数 ÷ 2 * * ( 3) 等 差 数 列 的 项 数 =( 末 项 -首 项 ) ÷公 差 +1 ( 4) 等 差 数 列 的 末 项 =首 项 +公 差 ×( 项 数 -1) 三 : 经 典 例 题 例 1、 11111111 22 33 44 55 66 77 8 (例 1、例 2、例 3 的 运算符号都是加号相连,分母都可以分解为两个连续正整数 的 积可用公 式111(n 1)1nnn) 例 2、 1111111261220304256 例 3、1111111111+3+5+7+9+11+13+15+17+19612203042567290110 * * 例 4、1111111 33 55 77 99 1111 13 例 5、 11111315356399 例 6、111111 +3+5+7+9315356399 * * 例 7、 11111++++144771 01 01 31 31 6 例 8、 22222+++++...